Если временные ряды рассматривать как некую совокупность данных, то по ним можно рассчитать ряд средних величин. Эти средние величины бывают нескольких типов.
Средний уровень интервального временного ряда с равноотстоящими уровнями рассчитывается по формуле средней арифметической простой
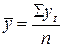 . (8.11)
. (8.11)
Пример 8. 3. В январе фирма реализовала продукцию на 100, в феврале – на 80, в марте – на 120 млн. руб. Это ряд интервальный (так как показатели реализации даны за месяцы) и равноотстоящий (так как использованы последовательно расположенные месяцы). Среднемесячный объем реализации в I квартале
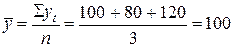 млн. руб.
млн. руб.
Средний уровень интервального временного ряда с неравноотстоящими уровнями и рассчитывается по формуле средней арифметической взвешенной. В качестве весов используется интервал времени 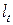 между уровнями временного ряда.
между уровнями временного ряда.
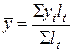 , (8.12)
, (8.12)
где 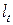 − интервал времени между уровнями ряда.
− интервал времени между уровнями ряда.
Пример 8.4. В январе фирма реализовала продукцию на 100, в марте – на 120, в июне – на 160 млн. руб. Среднемесячный объем реализации продукции в I полугодии
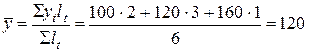 млн.руб.
млн.руб.
В задаче имеются данные не за все месяцы, поэтому при расчете среднемесячного объема реализации сделано предположение, что в пропущенные интервалы времени (месяцы) объем реализации оставался равным объему реализации за предыдущий известный месяц. Таким образом в феврале объем реализации будет равен январскому объему (100 млн. руб.), а в апреле и мае – мартовскому объему (120 млн. руб.). Кроме того, данный ряд является неравноотстоящим, так как между январем и мартом интервал времени равен 2 (январь имеет индекс 1, а март – 3, таким образом интервал равен 3–1=2), а между мартом и июнем интервал времени равен 3.
Средний уровень моментного временного ряда с равноотстоящими уровнями и рассчитывается по формуле средней хронологической простой
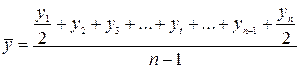 . (8.13)
. (8.13)
Пример 8.5. Остатки продукции на складе готовой продукции фирмы на 1 января 2003г. составили 24, на 1 февраля – 21, на 1 марта – 15, на 1 апреля – 18 шт. Данный ряд является моментным (данные приведены на определенный момент времени) с равноотстоящими уровнями ряда. Среднемесячные остатки в I квартале
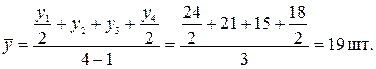
Средний уровень моментного временного ряда с неравноотстоящими уровнями и рассчитывается по формуле средней хронологической взвешенной
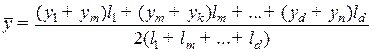 . (8.14)
. (8.14)
Пример 8.6. Остатки продукции на складе готовой продукции фирмы на 1 января составили 22, на 1 марта – 21, на 1 июня – 17, на 1 ноября – 19 шт. Среднемесячные остатки продукции на складе готовой продукции фирмы за 10 месяцев
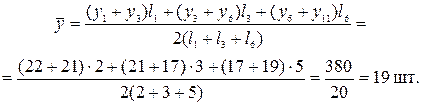
 2015-06-28
2015-06-28 2204
2204
