Уровни временного ряда отражают изменения, колебания экономического показателя во времени. Сами колебания обусловлены воздействием на показатель большого числа разнообразных факторов (спроса, конъюнктуры, моды, погоды, состояния основных средств и т.д.).
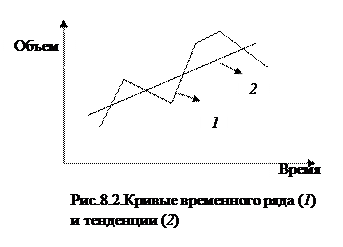
Под действием одних факторов изменения экономического показателя могут быть выражены в виде некоторой тенденции, т.е. в виде направленного развития экономического показателя во времени. Из анализа графика временного ряда на рис. 8.2 можно сделать вывод: хотя временной ряд (кривая 1) и колеблется, но значения уровней ряда имеют тенденцию увеличиваться во времени (кривая 2). Под действием других факторов колеблемость временного ряда может носить случайный характер, т.е в ряде будет отсутствовать тенденция.
 На практике временные ряды имеют и тенденцию, и случайность. Существуют несколько видов тенденций: тенденция средней, тенденция дисперсии и тенденция автокорреляции. Мы будем рассматривать только тенденцию средней. Тенденция средней (среднего уровня) – это изменение уровня ряда во времени в среднем. Она может состоять из тренда, сезонной и циклической компонент.
На практике временные ряды имеют и тенденцию, и случайность. Существуют несколько видов тенденций: тенденция средней, тенденция дисперсии и тенденция автокорреляции. Мы будем рассматривать только тенденцию средней. Тенденция средней (среднего уровня) – это изменение уровня ряда во времени в среднем. Она может состоять из тренда, сезонной и циклической компонент.
Тренд – это плавно изменяющаяся нециклическая кривая (прямая), описывающая действия основных долговременных факторов, эффект которых сказывается постепенно. Например, рост в среднем объема реализации продукции, снижение себестоимости продукции и т.д. Кривая 2 на рис. 8.2. является трендом временного ряда (кривая 1). Сезонная компонента – это циклическое изменение в среднем уровней ряда с периодом, равным одному году. Например, сезонное изменение цен на продовольственные товары. Циклическая компонента – это циклическое изменении в среднем уровней ряда с периодом, большим одного года. Например, периодическое обновление основных средств (основных фондов). Знание тенденции средней (среднего уровня) позволяет не только понять развитие экономического процесса во времени, но и осуществить прогнозирование.
Тренд во временном ряде может иметь различную форму, с учетом которой и выбирается соответствующий тип трендовой модели. Отметим основные типы трендовых моделей:
а) линейная трендовая модель 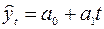 ;
;
б) параболическая 2-го порядка трендовая модель 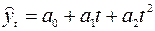 ;
;
в) степенная трендовая модель 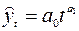 ;
;
г) показательная трендовая модель 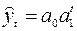 и т.д.
и т.д.
В рассмотренных трендовых моделях 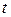 является независимым показателем – фактором,
является независимым показателем – фактором, 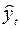 – зависимым показателем,
– зависимым показателем, 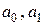 – параметрами модели.
– параметрами модели.
Чтобы выбрать соответствующую сущности изменения временного ряда трендовую модель, необходимо выполнить ряд последовательных действий.
1. Оценить однородность и сопоставимость уровней временного ряда.
2. Построить график временного ряда, по которому необходимо визуально оценить наличие или отсутствие тенденции средней в ряде и ее вид (тренд,сезонная или циклическая компоненты). Если по графику сложно определить наличие тенденции в ряде, то необходимо осуществить сглаживание временного ряда, например, методом скользящей средней. По сглаженным уровням ряда необходимо построить график и опять визуально оценить наличие тенденции.
Метод скользящей средней позволяет снизить колеблемость уровней ряда, в результате чего имеющаяся тенденция средней может быть более наглядно выражена. Для сглаживания ряда целесообразно использовать нечетный интервал сглаживания (3 или 5).
Таблица 8.4
| Обозна-чения ряда | Исход-ный ряд уt | Сглажен-ный ряд yt c |
| y1 y2 y3 y4 y5 | – 6,3 – |
Пример 8.11. Осуществим сглаживание временного ряда, приведенного в табл. 8.4, с помощью интервала сглаживания, равного 3. Рассчитаем первый уровень сглаженного ряда 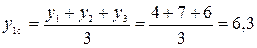 . Результат расчета запишем по центру интервала сглаживания, т.е. напротив y 2. Затем рассчитаем второй уровень сглаженного ряда
. Результат расчета запишем по центру интервала сглаживания, т.е. напротив y 2. Затем рассчитаем второй уровень сглаженного ряда 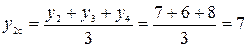 . Результат расчета запишем по центру интервала сглаживания, т.е. напротив y 3.
. Результат расчета запишем по центру интервала сглаживания, т.е. напротив y 3.
И, наконец, рассчитаем третий уровень сглаженного ряда 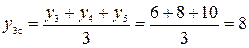 . Результат расчета запишем по центру интервала сглаживания, т.е. напротив y 4. Характер изменения сглаженных уровней ряда (6,3; 7; 8) показывает явную тенденцию роста; с учетом этого можно сделать вывод: исходный ряд имеет тенденцию средней, которая визуально соответствует тренду (т.е. прямой линии). Этот вывод будет более убедителен, если построить графики обоих рядов (студентам выполнить самостоятельно). Недостатком данного метода является то, что сглаженный ряд имеет меньшее число уровней ряда, чем исходный.
. Результат расчета запишем по центру интервала сглаживания, т.е. напротив y 4. Характер изменения сглаженных уровней ряда (6,3; 7; 8) показывает явную тенденцию роста; с учетом этого можно сделать вывод: исходный ряд имеет тенденцию средней, которая визуально соответствует тренду (т.е. прямой линии). Этот вывод будет более убедителен, если построить графики обоих рядов (студентам выполнить самостоятельно). Недостатком данного метода является то, что сглаженный ряд имеет меньшее число уровней ряда, чем исходный.
3. Если предварительно установлено, что временной ряд содержит тенденцию средней, например, в виде тренда, то далее надо определить тип трендовой модели (линейная, нелинейная – параболическая, степенная, показательная и т.д.). Для этого, опять-таки на основе анализа графика временного ряда, необходимо выбрать несколько предполагаемых типов трендовых моделей. Например, визуальный анализ временного ряда показывает, что имеющийся тренд можно выразить с помощью линейной или параболической модели. Затем по каждой модели необходимо рассчитать ее параметры. Зная параметры каждой модели, можно оценить, какая из выбранных моделей наилучшим образом аппроксимирует исходный временной ряд.
Для нахождения параметров трендовых моделей может быть использован метод наименьших квадратов (МНК). Рассмотрим его применение.
Линейная трендовая модель 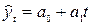 используется тогда, когда цепные абсолютные приросты уровней ряда приблизительно равны по модулю. Для нахождения параметров линейной модели (
используется тогда, когда цепные абсолютные приросты уровней ряда приблизительно равны по модулю. Для нахождения параметров линейной модели (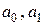 ) необходимо составить систему линейных уравнений
) необходимо составить систему линейных уравнений
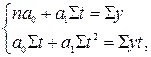 (8.19)
(8.19)
 2015-06-28
2015-06-28 8307
8307
