1. Новиков Ф.А. Дискретная математика для программистов. – СПб.: Питер, 2001. - С.47-49.
2. Кук Д., Бейз Г. Компьютерная математика. – М.: Наука, 1990. - С.64-68.
3. Глушков В.М., Цейтлин Г.Е., Ющенко Е.Л. Алгебра, языки, программирование. – К.:Наукова думка, 1989. - С.56-64.
Додаткова
4. Сигорский В.П. Математический аппарат инженера. – К.: Техника, 1975. - С.137-145.
5. Коршунов Ю.М. Математические основы кибернетики. – М.: Энергоатом-издат, 1987. - С.62, 63.
6. Горбатов В.А. Основы дискретной математики. – М.: Высш.шк., 1986. - С.13-20.
7. Биркгоф Г., Барти Т. Современная прикладная алгебра. – М.: Мир, 1976. - С.16-25.
Для практичних занять
8. Методичні вказівки і завдання до контрольних робіт з дисципліни «Основи дискретної математики» для студентів очної та заочної форм навчання фахів 6.0804, 6.0915 / О.М. Мартинюк. – Одеса: ОНПУ, 2001. – С.18-21.
Лекція 10. Закони композиції
Вступ
Лекція має за мету навести загальні поняття композиції об'єктів. Розглянуто закони композиції, у тому числі внутрішні й зовнішні, визначений групоід, спеціальні елементи, адитивні й мультиплікативні позначення. Звернено увагу на властивості внутрішнього закону композиції.
|
|
|
У лекції присутні два підрозділи:
10.1. Композиція об'єктів
10.2. Внутрішній закон композиції
10.1 Композиція об'єктів
10.1.1. Основні визначення
Велике значення мають відношення, що ставлять у відповідність парі яких-небудь об'єктів (а, b) третій об'єкт с. Прикладами таких відношень є дії над числами. У загальному випадку відношення може являти собою деяку операцію не тільки між числами, але й між об'єктами будь-якої природи. При цьому запис а Т b = с, або a ^ b = с, означає, що а в композиції з b дає с. Символ Т (або ^) позначає операцію, об'єкти а й b називають операндами, а об'єкт с – результатом операції, або композицією об'єктів а й b.
Нехай множини операндов позначені відповідно через А и В (аÎА і bÎВ), а множина результатів операції - через C (cÎC). Тому що множина всіх пар (а, b) є прямим добутком А´В, то операцію визначають як відображення множини А´В у С, тобто А´В®С, і часто називають законом композиції.
Любой закон композиції А´В®С над скінченними множинами можна задавати прямокутною матрицею (таблицею Кели). Рядки таблиці відповідають елементам множини А, стовпці - елементами множини В. На перерізанні рядка й стовпця, що відповідає парі (а, b), розташовується елемент с = а Т b.
Приклад. Таблиці додавання й множення однорозрядних чисел є прикладами таблиць Кели.
У загальному випадку таблиця для бінарної операції має вигляд
Таблиця 10.1
| T | b1 | b2 | b3 | b4 | … |
| a1 | c11 | c12 | c13 | c14 | … |
| a2 | c21 | c22 | c23 | c24 | … |
| a3 | c31 | c32 | c33 | c34 | … |
| … | … | … | … | … | … |
10.1.2. Закони композиції на множині
|
|
|
Множини А, В, С, що беруть участь в операції А´В®С, не обов'язково повинні бути різними. Якщо В = С = S, то говорять, що закон композиції визначений на множині S.
Розрізняють внутрішній закон композиції S´S®S і зовнішній закон композиції й W´S®S, де W і S - різні множини. У випадку внутрішнього закону говорять, що множина утворить групоїд щодо операції Т. У випадку зовнішнього закону композиції елементи wÎW називають операторами, a W - множиною операторів на множині S.
Приклад. Внутрішній закон композиції являють додавання а+b = с і множення ab = с на множині дійсних чисел, а також геометричне підсумовування векторів на площині.
Приклад. Множення вектора на скаляр може бути прикладом зовнішнього закону композиції на множині векторів, причому операторами є скаляри, що як елементи належать множині дійсних чисел.
Приклад. Нехай S – множина диференційовних функцій f(xl, х2,..., хn) і W — множина операторів диференціювання ¶/¶хi (i = 1, 2,..., n). Тоді парі (¶/¶хi, fI) можна поставити у відповідність частинну похідну ¶f/¶хi, тобто визначити зовнішній закон композиції на множині диференційовних функцій.
Далі будуть розглядатися в основному тільки внутрішні закони композиції.
10.1.3. Матриця й граф групоїда
Скінченний групоїд S щодо закону Т визначається квадратною матрицею n-ro порядку (n - число елементів групоїда).
Приклад. Скінченний групоїд, заданий матрицею 4-го порядку
Таблиця 10.2
| T | a | b | c | d |
| a | b | c | a | b |
| b | a | b | c | a |
| c | b | a | d | d |
| d | d | b | d | b |
Побудова графу групоїда заснована на представленні бінарного співвідношення а Т b = с (рис. 10.1,а), де дуги графу зображують елементи а, b, с Î S, причому операнди утворюють деякій шлях, а дуга результату операції замикає цей шлях. Якщо a Т b = а, то b зображується петлею в скінченній вершині дуги а. При побудові графу спочатку наносять дуги для всіх елементів групоіда як вихідні з однієї вершини, а потім послідовно зображують всі бінарні співвідношення.
Приклад. На рис. 10.1,б представлений граф групоіда, що заданий наведеною вище матрицею. Дуги а, b, с, d, що виходять із однієї вершини, відповідають елементам групоіда. Тому що а Т а = b, а Т b = с, а T с = a і a T d = b, то з кінця дуги а проводять дуги а, b, с, d відповідно до скінченних вершин дуг b, с, а, b. Дві паралельні дуги а й d, спрямовані до скінченної вершини дуги b, умовно зображують однією дугою a, d. Дуга с починається й кінчається в скінченній вершині дуги а, тобто утворить петлю. Аналогічно зображують на графі й інші співвідношення, обумовлені матрицею групоїда.
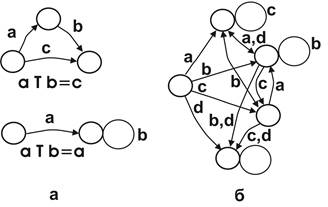
Рис. 10.1. Граф операції; частина а — операнди a, b
і результат операції с; частина б — граф групїда
 2015-06-28
2015-06-28 337
337








