Загальні визначення операцій

Деякі функції використовують при введенні позначень.

Визначення. Операцією над множиною S називається функція f: Sⁿ®S, де nÎN і є два важливих моменти операції: а) однозначність ½f(1)½£1; б) замкнутість на S.

Операція Sⁿ®S має порядок n. Якщо n=1, то операція одномісна (унарна, монадічна), якщо n=2, то операція двомісна (бінарна, діадічна). Компоненти s₁, s₂,…,s_i,…,s_n з набору (вектора) (s₁, s₂,…,s_i,…,s_n)ÎSⁿ називають операндами, самі символи операцій називають операторами. Інший підхід, наприклад, у програмуванні, розуміє під операторами операнди, зв'язані символами операцій у формули.

Приклад. Бінарною операцією є додавання, або добуток на множині дійсних чисел D, унарною операцією є ступень на множині D. N-арною операцією є додавання виразів звичайної мови з інших виразів.

У випадку одномісних операцій символ оператора ставлять звичайно перед, або після операнда, у випадку двомісних операцій можливі три способи: а) infix (інфікс) - оператор розміщується між операндами;
б) prefix (префікс) - оператор розміщується перед операндами; в) postfix (постфікс) - оператор розміщується після операндов.

Приклад. a+b - infix;

+ab - prefix;

ab+ - postfix

Форми prefix і postfix не вимагають дужок при визначенні порядку обчислень складних виражень, що робить їх зручними для автоматичної обробки.

Приклад. a+b*c+(d+e*(f+g)) - infix;

++a*bc+d*e+fg - prefix;

abc*+defg+*++ - postfix

а) (((a+(b*c))+(d+(e*(f+g)))) - infix:

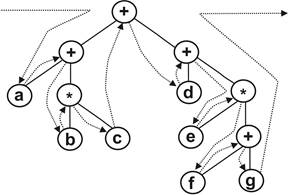
Рис. 9.1. Інфіксна форма запісу

б) ++a*bc+d*e+fg - prefix:

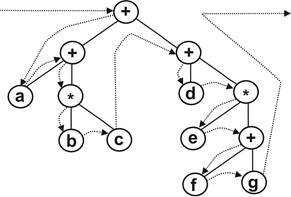
Рис. 9.2. Префіксна форма запісу

в) abc*+defg+*++ - postfix:

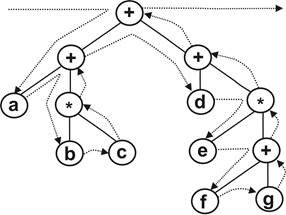
Рис. 9.3. Постфіксна форма запісу

Нехай Å позначається як адитивна операція (типу додавання), а Ä - як мультиплікативна операція (типу множення).

9.3.2. Властивості операцій

1. aÅb=bÅa; aÄb=bÄa комутативність.

2. aÅ(bÅc)=(aÅb)Åc; aÄ(bÄc)=(aÄb)Äc асоціативність.

3. аÅ(bÄc)=(aÅb)Ä(aÅc); aÄ(bÅc)=(aÄb)Å(aÄc) дистрибутивність.

4. аÅа=а; аÄа=а ідемпотентність.

5. Якщо для всіх елементів аÎA існує bÎA такий, що а) bÄa=a (bÅa=a), то b – ліва одиниця (лівий нуль); б) aÄb=a (aÅb=a), то b – права одиниця (правий нуль); в) одночасно aÄb=a (aÅb=a) і bÄa=a (bÅa=a), то b – двостороння одиниця (нуль) по операції Ä (Å).

6. Якщо е – одиниця (нуль) і хÄу=е (хÅу=е), то х – лівий обернений елемент до у, у – правий обернений елемент до х, якщо хÄу=е (хÅу=е) і вÄх=е (уÅх=е), то х и у – обернені елементи по відношенню друг до друга.

Лема. Нехай Ä (Å) – мультиплікативна (адитивна) операція на множини А і існує одиниця (нуль) стосовно операцій Ä (Å). Одиничний (нульовий) елемент тільки один.

Лема. Нехай Ä (Å) – асоціативна операція на множини А и е – одиниця (нуль) стосовно Ä (Å). Тоді, якщо аÎA і є обернений елемент, то обернений елемент тільки один стосовно операцій Ä (Å).

Приклад. A={1, 2, 3, 4}; B={3, 4, 5}; С ={1, 3};

AÈB=BÈA={1, 2, 3, 4, 5} і AÇB=BÇA={3, 4}
– комутативність;

AÈ(BÈС)=(AÈB)ÈС={1, 2, 3,4, 5} і AÇ(BÇС)=(AÇB)ÇС={3} – асоциативність;

AÈ(BÇC)=(AÈB)Ç(AÈC)={1, 2,3, 4} і AÇ(BÈC)=(AÇB)È(AÇC)={1, 3, 4}
– дистрибутивність;

AÈA=A={1, 2, 3, 4} і AÇA=A={1, 2, 3, 4}
– ідемпотентність;

AÈÆ=A={1, 2, 3, 4} і ÆÈA=A={1, 2, 3, 4}
– двосторонній нуль;

AÇU=A={1, 2, 3, 4} і UÇA=A={1, 2, 3, 4}
– двостороння одиниця;

AÈ`A=U і AÇ`A=Æ, отже A і `A
– обернені елементи по відношенню один до одного.

Контрольні запитання

1. Як визначають транзитивне і рефлексивне замикання?

2. У чому суть методу Варшалла?

3. Яка підмножина А¢ множини А називається замкнутою щодо відповідності g?

4. Що є підстановкою, циклом? Які елементи є стаціонарними?

5. Що таке послідовність і у чому її різниця з функціоналом?

6. Як функції можуть зберегти алгебраїчні властивості?

7. Як визначається операція?

8. Що є одномісною, двомісною, n-місною операціями?

9. У чому різниця інфіксної, префіксної і постфіксної форм запису операцій?

10. Чому потрібні декілька форм?

11. Які властивості мають операції?

12. Що є ліва, права, двостороння одиниця, або нуль?

13. Що таке обернений елемент?