Поняття вектора і n-вимірного векторного простору

Вектори.

Відомо, що впорядкована множина n дійсних чисел називається n -вимірним вектором, а самі числа – компонентами (координатами) вектора. Позначається , .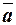

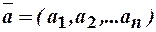Вектор, всі компоненти якого рівні нулю, називають нуль-вектором.

Два вектори називаються рівними, якщо попарно рівні їх відповідні компоненти: .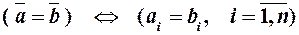

Сумою двох векторів називається вектор, кожна компонента якого дорівнює сумі відповідних компонент векторів доданків:

.

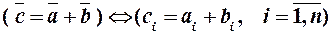Добутком вектора 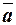на число 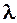називається вектор, кожна компонента дорівнює добутку відповідних компонент вектора 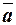на число : .

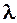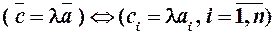Властивості операцій над векторами:

1. 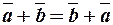(комутативність)

2. ,

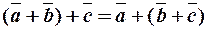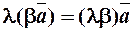(асоціативність)

3. ,

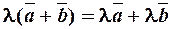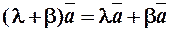(дистрибутивність)

Множина n -вимірних векторів на якій визначені дії додавання векторів і множення вектора на число, для яких виконуються властивості 1-3, називається n -вимірним векторним простором (Rⁿ).

Скалярним добутком векторів називається число, рівне сумі добутків одноімених координат векторів

.

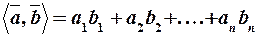Властивості скалярного добутку векторів:

1. 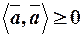, причому 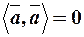, якщо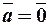

2.

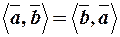
3.

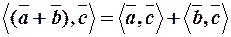
4.

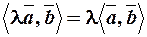
Число 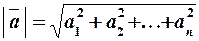називається модулем (довжиною) вектора .

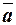Лінійний векторний простір називається Евклідовим, якщо в ньому визначено скалярний добуток, що задовольняє властивостям 1 - 4.