2014-02-02
11904
Векторное поле – это область пространства, в каждой точке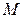 
которой задан вектор 
.
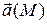Пример 1. Пусть на материальную точку в области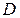 
действует сила 
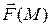. Тогда в области 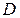определено векторное поле .
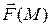Пример 2. Пусть в области 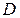происходит течение жидкости и в каждой точке 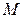задан вектор 
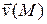скорости частицы жидкости. Тогда в области 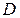определено векторное поле скоростей жидкости.
Пример 3. Поместим заряд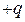 
в начало координат. Тогда сила, с которой этот заряд действует на единичный положительный заряд, помещенный в точку 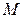, определяется по закону Кулона:
,
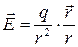где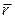 
- вектор, идущий из начала координат в точку 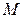(радиус-вектор точки ), 
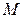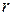- его длина. Имеем векторное поле напряженностей 
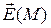, создаваемое зарядом 
.
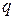Мы будем рассматривать только стационарные поля, для которых вектор поля 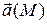зависит от точки 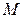и не зависит от времени. Проекции вектора 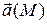на оси координат обозначим 
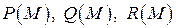. Тогда:
.
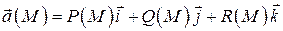Далее всюду предполагаем, что функции 
непрерывны вместе со своими частными производными; в противном случае точку поля назовем особой.
Одной из характеристик векторного поля являются векторные линии.
Векторной линией векторного поля называют линию, в каждой точке которой касательный вектор коллинеарен вектору поля (рис. 3).
Векторные линии в конкретных полях имеют ясный физический смысл.
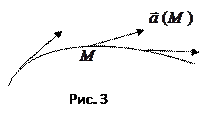В поле скоростей текущей жидкости векторные линии – это линии тока этой жидкости, т. е. линии, по которым движутся частицы жидкости.
В электрическом поле векторные линии – это силовые линии и их расположение очень важно в физике.
Выведем уравнения векторных линий для поля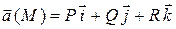 
(для краткости аргументы функций 
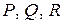не выписаны).
Пусть уравнения векторной линии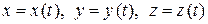 
, (
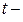параметр). Касательным вектором этой линии является вектор 
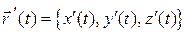и вектор 
.
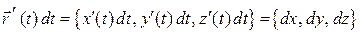По определению векторной линии ее касательный вектор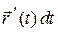 
и вектор поля 
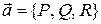коллинеарны. Поэтому координаты этих векторов пропорциональны, т. е.
.
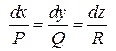Пример 4. Магнитное поле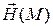 
создано электрическим током силы 
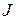, текущим по бесконечно длинному прямому проводу 
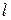. Найти силовые линии этого поля.
Решение. Если провод 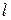принять за ось 
некоторой декартовой системы координат, то, как известно из физики,
.
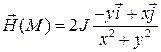Запишем уравнения векторных линий для поля :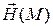
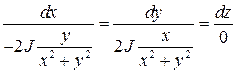или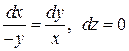 
.
Из первого уравнения имеем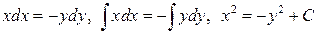 
. Из второго уравнения 
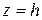. Таким образом, силовые линии поля 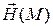есть окружности 
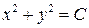, расположенные в плоскостях 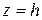, параллельных плоскости 
.
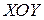Пример 5. Найти векторные линии поля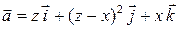 
.
Решение. Учитывая, что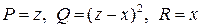 
, запишем систему:
.
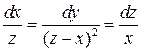В одном из уравнений этой системы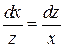 
разделим переменные: 
.
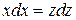Теперь проинтегрируем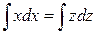 
и получим
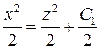или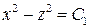 
.
Чтобы решить другое уравнение системы, воспользуемся известным свойством пропорций: если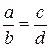 
, то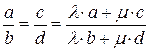 
. В нашем примере удобно взять 
, 
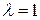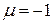и записать систему уравнений следующим образом:
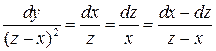или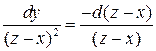 
.
Разделим переменные: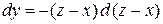 
. Проинтегрируем 
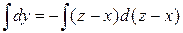и получим 
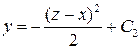. Таким образом, векторные линии данного поля есть линии пересечения поверхносте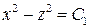й и .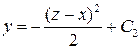
ПОТОК ВЕКТОРНОГО ПОЛЯ
Пусть в некоторой части пространства течет жидкость, причем скорость частицы жидкости зависит только от точки, через которую протекает жидкость, и не зависит от времени, т. е.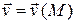 
. Требуется вычислить количество (объем) жидкости 
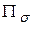, протекающее в единицу времени через ориентированную поверхность 
в выбранном направлении (предполагается, что жидкость может свободно протекать через эту поверхность).
Рассмотрим сначала простейший случай. Пусть - плоская площадка с нормальным вектором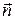 
, а скорость течения жидкости 
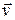во всех точках одна и 
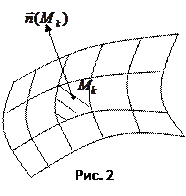та же. Тогда количество жидкости, 
протекающей через эту площадку в единицу времени, равно (рис. 1) объему цилиндра с основанием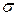 
и образующей 
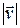. Так как высота этого цилиндра равна 
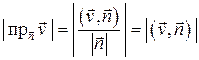, то его объем равен 
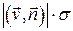. Эта величина и равна количеству жидкости, протекающей через . Опустив знак абсолютной величины, мы получим величину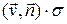 
, которую называют потоком жидкости через .
Если угол между векторам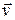и и 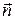- острый, то говорят, что жидкость течет в направлении вектора 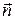; в этом случае 
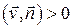и поток совпадает с количеством жидкости. Если угол между векторам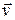и и 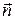тупой, то говорят, что жидкость течет в направлении, противоположном вектору 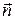; в этом случае 
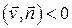и поток отличается от количества жидкости знаком.
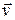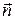Если векторы и перпендикулярны, то жидкость течет вдоль площадки и поток равен нулю.
Перейдем теперь к общему случаю. Для вычисления потока жидкости через произвольную поверхность разобьем эту поверхность на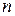 
частей 
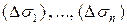с площадями 
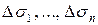(рис. 2).
На каждой площадке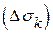 
выберем произвольную точку 
. Будем приближенно считать, что все частицы, протекающие через малую площадку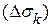 
, имеют одинаковые скорости 
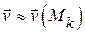; кроме того, площадку будем считать плоской и перпендикулярной нормальному вектору 
.
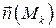Тогда поток жидкости через площадку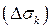 
приближенно равен
.
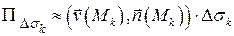Для потока через всю поверхность получим:
.
Это приближенное равенство будет тем точнее, чем меньше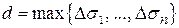 
. Точное значение потока определяется как предел этой суммы при 
:
.
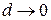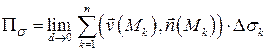Полученный предел равен поверхностному интегралу I рода от скалярной функции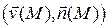 
. Таким образом, поток жидкости через поверхность вычисляется по формуле
.
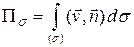Отметим, что
1) если суммарный поток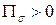 
, то количество жидкости, протекающей в направлении нормали 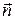, больше количества жидкости, протекающей в направлении 
;
2) если суммарный поток 
, то количество жидкости, протекающей в направлении нормали 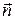, меньше количества жидкости, протекающей в направлении ;
3) если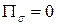 
, то количества жидкости, протекающей в том и другом направлении, одинаковы.
Интеграл в формуле (10.1) является поверхностным интегралом первого рода от скалярной функции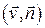 
. Его также называют поверхностным интегралом второго рода от вектор-функции 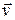. Аналогичным образом определяют поток и для произвольного векторного поля 
.
