Введенные выше операции обладают всеми обычными свойствами сложения и умножения чисел:
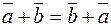 – коммутативность сложения;
– коммутативность сложения;
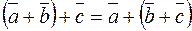 – ассоциативность сложения;
– ассоциативность сложения;
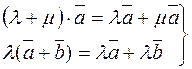 – дистрибутивность умножения относительно сложения;
– дистрибутивность умножения относительно сложения;
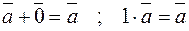 и т.п.
и т.п.
Эти свойства дают право при умножении скалярного многочлена на векторный многочлен производить умножение “почленно”.
Замечание. Согласно определению векторы  и
и 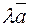 коллинеарные. Оказывается, справедливо и, в некотором смысле, обратное утверждение, а именно:
коллинеарные. Оказывается, справедливо и, в некотором смысле, обратное утверждение, а именно:
если вектор  коллинеарен ненулевому вектору
коллинеарен ненулевому вектору 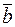 , то существует и притом единственное, число λ такое, что
, то существует и притом единственное, число λ такое, что 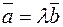 . Попробуйте доказать это утверждение, взяв
. Попробуйте доказать это утверждение, взяв 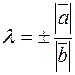 , где знак “+” соответствует
, где знак “+” соответствует 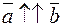 , а знак “–” соответствует
, а знак “–” соответствует 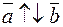 .
.
 2015-06-28
2015-06-28 843
843








