Проекции вектора на оси. Направляющие косинусы

Рассмотрим некоторую ось u и выберем какой-нибудь отрезок в качестве единицы измерения длин. Если нам дан некоторый вектор , то поместим его начало в какую-нибудь точку О оси u, а конец вектора пометим буквой А. Пусть далее В – какая-нибудь точка оси u, расположенная в положительном направлении от точки О.

Угол 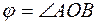называют углом наклона вектора к оси u. Этот угол понимаем в элементарно-геометрическом смысле, пределы изменения от 0 до π.

Проекцией вектора на ось u называют число

,

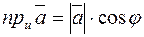где φ – угол наклона к оси u.

Это число имеет наглядный геометрический смысл. Спроектируем начало и конец вектора 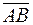на ось u, получим точки А ₁, В ₁. Рассмотрим вектор 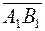лежащий на оси u. Тогда

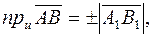
причем знак “+” соответствуем случаю, когда угол φ острый, а “–”, когда φ – тупой.

В

φ

А

А ₁ В ₁ u

Элементарно-геометрическими методами можно получить свойства проекций вектора на ось:

.

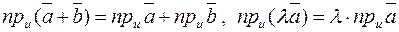Замечание 1. Если φ – это угол между векторами и 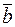(понимаемый как угол между двумя отрезками, исходящими из одной точки), то число 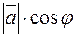называют проекцией вектора на направление вектора 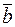, или просто проекцией на 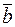и обозначают символом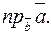

Пусть теперь на плоскости (или в пространстве) задана ДПСК. Проекции вектора на оси координат обозначают а_x, a_y, a_z, или a ₁, a ₂, a ₃, или X, Y, Z. Проекции вектора на оси координат, будучи заданы, вполне определяют его как свободный вектор, т.е. с точностью до положения в пространстве. Если вектор расположен в плоскости xOy, то достаточно двух проекций a ₁ и a ₂. Проекции вектора часто называют его координатами.

Тот факт, что вектор имеет проекции a ₁, a ₂, a ₃, показывают записью

.

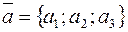Итак, впредь для нас вектор, чаще всего, это упорядоченная тройка (или пара) чисел.

Если вектор задан началом A (x ₁; y ₁; z ₁) и концом B (x ₂; y ₂; z ₂), то его проекции определяются формулами

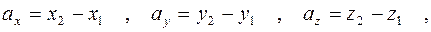т.е.

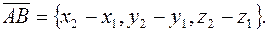
Выразим линейные операции над векторами через их проекции. Пусть 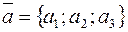, 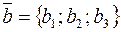. Тогда:

1. 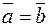тогда и только тогда когда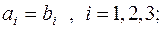

2.

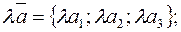
3.

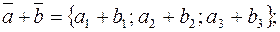
4. условие коллинеарности: 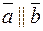тогда и только тогда, когда

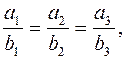т.е. проекции пропорциональны;

5.

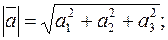
6. условие компланарности векторов , 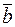и :

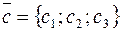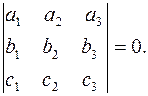
Обозначим через 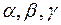углы, которые вектор составляет с осями абсцисс, ординат и аппликат соответственно. Направляющими косинусами вектора называют косинусы этих углов. Очевидно (из определения проекций):

.

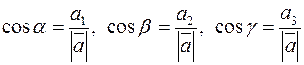Основное свойство направляющих косинусов:

.

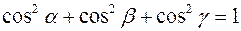Кроме того, направляющие косинусы вектора служат проекциями орта этого вектора:

.

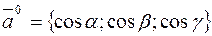Замечание 2. Вектор можно задавать: 1) длиной и направлением (т.е. углами 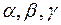); 2) началом и концом; 3) проекциями. Необходимо уметь переходить от одного способа к другому.