Некоторые физические величины, такие как скорость, ускорение, сила, характеризуются не только числовым значением, но и направлением. Они называются векторными величинами. Математической моделью такой величины служит вектор.
Вектором называют направленный отрезок, т.е. отрезок, для которого указано, какая из ограничивающих его точек считается началом, а какая концом.
На чертежах векторы обозначаются в виде стрелки →. В тексте вектор записывается либо двумя большими буквами с общей чертой наверху 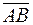 (первая из них – это начало, а вторая – конец), либо одной малой буквой с чертой
(первая из них – это начало, а вторая – конец), либо одной малой буквой с чертой  , либо малой буквой полужирного шрифта a.
, либо малой буквой полужирного шрифта a.
Длиной вектора или модулем называется длина отрезка изображающего вектор. Обозначение 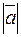 ,
, 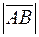 иногда АВ.
иногда АВ.
Вектор, длина которого равна нулю (т.е. конец совпадает с началом) называется нулевым: 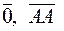 . Направление нулевого вектора следует считать вполне неопределенным. (нулевой вектор можно считать перпендикулярным любому вектору и коллинеарным любому вектору).
. Направление нулевого вектора следует считать вполне неопределенным. (нулевой вектор можно считать перпендикулярным любому вектору и коллинеарным любому вектору).
Единичным вектором, или ортом, называют вектор, длина которого равна 1.
Векторы, лежащие на одной прямой, или на параллельных прямых, называются коллинеарными. Обозначение:  | |
| | 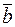 . Коллинеарные векторы, направленные в одну сторону, называются одинаково направленными, а направленные в противоположные стороны – противоположно-направленными. Обозначения:
. Коллинеарные векторы, направленные в одну сторону, называются одинаково направленными, а направленные в противоположные стороны – противоположно-направленными. Обозначения: 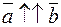 ,
, 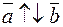 .
.
Векторы  и
и 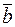 называют равными и пишут
называют равными и пишут 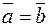 , если: 1)
, если: 1) 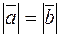 (имеют равные длины); 2)
(имеют равные длины); 2) 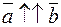 (одинаково направлены).
(одинаково направлены).
Такое определение равенства векторов означает, что векторы рассматривают с точностью до их положения на плоскости, в пространстве, т.е. не различая векторов, получающихся друг из друга параллельным переносом. В этом смысле векторы называют свободными. Точка приложения вектора – его начало – может быть выбрана произвольным образом.
Три вектора называются компланарными, если лежат в одной плоскости, или в параллельных плоскостях. В противном случае они называются некомпланарными.
Нетрудно доказать такие утверждения:
1. Если  | |
| | 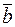 , то
, то  ,
, 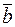 ,
, 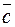 – компланарные (для любого
– компланарные (для любого 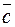 ).
).
2. Векторы 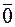 и
и  коллинеарные;
коллинеарные; 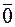 ,
,  ,
, 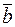 , – компланарные (для любых
, – компланарные (для любых  и
и 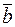 ).
).
3. Если  ,
, 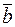 ,
, 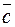 некомпланарные, то любые два из них некол- линеарные.
некомпланарные, то любые два из них некол- линеарные.
 2015-06-28
2015-06-28 1318
1318








