Пусть известны проекции векторов на оси некоторой ДПСК: 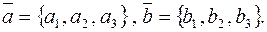 Запишем разложения этих векторов по базису
Запишем разложения этих векторов по базису 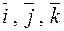 :
:
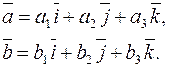
Базисные векторы – единичные, значит, их скалярные квадраты равны 1; они взаимно перпендикулярные значит 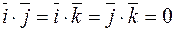 . Перемножая разложения почленно, получим
. Перемножая разложения почленно, получим
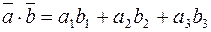 . (3)
. (3)
Это и есть формула, выражающая скалярное произведение векторов через их проекции на оси ДПСК.
Из формулы (3) можно получить ряд важных следствий.
1. Длина вектора 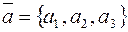 вычисляется по формуле
вычисляется по формуле
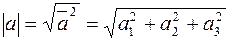 .
.
2. Угол φ между векторами 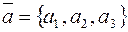 и
и 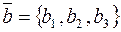 определяется равенством
определяется равенством
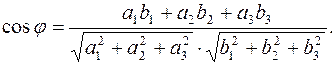
3. Необходимым и достаточным условием перпендикулярности векторов 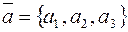 и
и 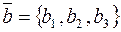 является равенство
является равенство
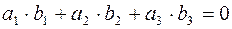 .
.
4. Если ось и составляет с осями координат углы 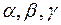 , то проекция вектора
, то проекция вектора 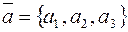 на эту ось определяется равенством
на эту ось определяется равенством
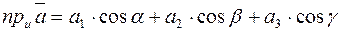 . (4)
. (4)
Для доказательства (4) рассмотрим единичный вектор 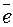 одинаково направленный с осью и. Тогда: 1)
одинаково направленный с осью и. Тогда: 1) 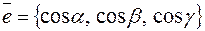 ; 2)
; 2) 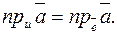 Но из определения
Но из определения 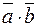 следует
следует
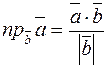 .
.
Остается в этой формуле положить 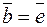 и воспользоваться формулой (3)
и воспользоваться формулой (3)
и тем, что 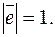
5. Если 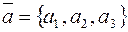 , то
, то 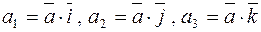 .
.
 2015-06-28
2015-06-28 1620
1620








