II Свойства скалярного произведения

1. 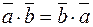(коммутативность).

2. 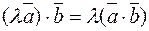(ассоциативность относительно умножения на

число).

3. 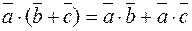(дистрибутивность относительно сложения).

Замечание 1. Указанные свойства дают право при скалярном перемножении векторных многочленов выполнять действия почленно, не заботясь о порядке сомножителей. Например,

Замечание 2. Скалярного произведения трех векторов не существует.

4. Скалярное произведение 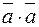называется скалярным квадратом вектора и обозначается символом 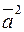. Скалярный квадрат вектора, равен квадрату его длинны:

.

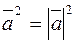Это свойство можно использовать для нахождения длин векторов. Например, найти длину вектора 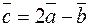, где 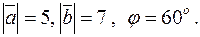Имеем:

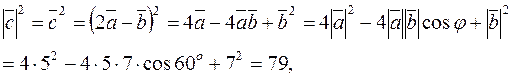
откуда .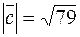

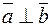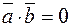5. Если , то (т.к. 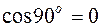), но важно и обратное утверждение: если 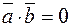, то векторы взаимно перпендикулярны. Действительно, равенство 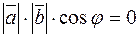возможно, если: 1) 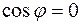, или 2) 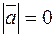, или 3) 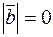. В первом случае сразу получаем 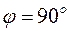. Второй (третий) случай означает, что вектор (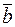) есть нулевой вектор, направление которого можно считать каким угодно, в частности перпендикулярным .

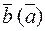Сказанное выше можно сформулировать как условие перпендикулярности векторов:

векторы перпендикулярны тогда и только тогда, когда их скалярное произведение равно 0.