2015-06-28
599
Векторы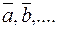 
называются линейно независимыми, если ни один из них не является линейной комбинацией других. Для двух векторов незави- симость равносильна неколлинеарности, а для трех – некомпланарности.
Говорят, что линейно независимые векторы образуют базис, если любой другой вектор является их линейной комбинацией.
Теорема 2. Любая тройка некомпланарных векторов образует базис в пространстве. Любая пара неколлинеарных векторов образует базис в плос- кости, содержащей эту пару векторов.
Другими словами, если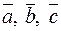 
– некомпланарные векторы, то для любого вектора 
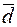существуют (и притом единственные) числа 
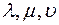такие, что
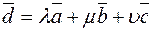. (2)
Поиск коэффициентов линейной комбинации (2) сводится к решению системы линейных уравнений, матрица коэффициентов которой составлена из проекций векторов 
, 
, 
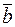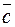(по столбцам), а свободные члены – это
проекции вектора .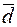
Замечание к §3-6.
Студент должен уметь:
– выполнять действия с векторами в геометрической и координатной формах;
– находить проекции, длину, направляющие косинусы, орт вектора;
– разлагать вектор по базису;
– проверять коллинеарность и компланарность векторов.
ЛЕКЦИЯ 5
