2015-06-28
309
Векторная алгебра. Векторы.
Существуют скалярные и векторные величины. Скалярные характеризуются своим численным значением (например, температура, работа, плотность,…), а векторные, кроме численного значения, обладают также направлением в пространстве (например, сила, скорость,…).
Определение 1. Вектором называется направленный отрезок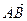 
с начальной точкой А и конечной В.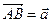 
Начало вектора называется его точкой приложения.
Определение 2. Длиной вектора 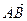называется длина отрезка 
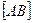. Число, равное длине вектора, измеренного выбранной масштабной единицей, называется модулем.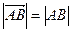 
Задать вектор – это значит задать его модуль и направление в пространстве.
Определение 3. Вектор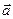 
называется единичным, если 
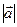=1. Вектор 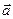называется нулевым или нуль-вектором, если 
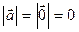. Нулевой вектор 
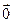имеет любое направление.
Определение 4. Векторы 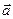и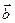 
называются сонаправленными, если они параллельны (лежат на одной или параллельных прямых) и имеют одинаковое направление, если при этом направление не совпадает, то векторы называются противоположно направленными.
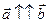– сонаправлены. 
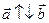– противоположно направлены.
Определение 5. Векторы 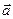и 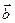называются равными, если 
.
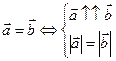Определение 6. Единичный вектор, имеющий одинаковое направление с вектором 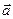, называется ортом вектора 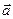и обозначается 
.
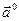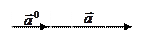
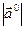=1.
Определение 7. Вектор, выходящий из начала координат, называется радиус-вектором.
С помощью параллельного переноса векторы можно перемещать в любое место пространства.
