Определение 9. Пусть λ – действительное число, тогда произведением числа λ на вектор 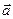 называется вектор
называется вектор 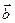 такой, что 1)
такой, что 1) 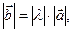 2)
2) 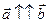 , если
, если 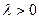 и
и 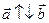 , если
, если 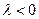 .
.
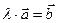 , причем
, причем 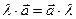 .
.
Умножение вектора на число – это растяжение или сжатие вектора с сохранением или с изменением на противоположное направления.
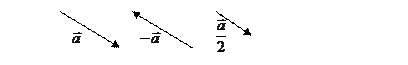
Свойства произведения: 1. 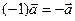 2.
2. 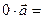
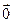 3.
3. 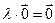 4.
4. 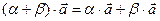
5. λ (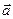 +
+ 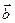 ) = λ
) = λ 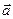 + λ
+ λ 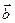 6.
6. 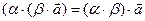 7.
7. 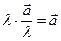 8.
8. 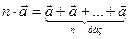
Определение 10. Векторы, лежащие на одной или параллельных прямых, называются коллинеарными.
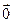 коллинеарен любому вектору.
коллинеарен любому вектору.
Теорема 1 (о необходимом и достаточном условии коллинеарности векторов). Равенство 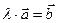 , где λ – действительное число, справедливо тогда и только тогда, когда векторы
, где λ – действительное число, справедливо тогда и только тогда, когда векторы 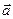 и
и 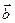 коллинеарны, при этом если
коллинеарны, при этом если 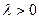 , то
, то 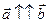 , если
, если 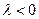 , то
, то 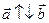 , если λ = 0, то направление
, если λ = 0, то направление 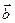 любое.
любое.
 2015-06-28
2015-06-28 272
272








