Вопросы:
- Основные понятия.
- Операции над векторами, их свойства.
- Проекция вектора на ось.
- Разложение вектора по ортам координатных осей. Координаты вектора.
- Модуль вектора. Действия над векторами, заданными координатами. Скалярное произведение векторов. Свойства скалярного произведения. Выражение скалярного произведения через координаты. Некоторые приложения скалярного произведения.
1.
Величины, которые полностью определяются своим численным значением, называют скалярными. Примерами скалярных величин являются: площадь, длина, объем, температура, работа, масса.
Другие величины, например сила, скорость, ускорение, определяются не только своим числовым значением, но и направлением. Такие величины называют векторными. Векторная величина геометрически изображается с помощью вектора.


Вектор – это направленный прямолинейный отрезок, т.е. это отрезок, имеющий определенную длину и направление. Если А начало вектора, а В – его конец, то вектор обозначают 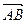 или
или  . Вектор
. Вектор 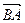 (у него начало в точке В, а конец в точке А) называют противоположным вектору
(у него начало в точке В, а конец в точке А) называют противоположным вектору 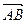 . Вектор противоположный вектору
. Вектор противоположный вектору  , обозначается -
, обозначается -  .
.

Длиной или модулем вектора 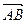 называют длину отрезка и обозначают
называют длину отрезка и обозначают 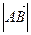 . Вектор, длина которого равна нулю, называют нулевым вектором и обозначают
. Вектор, длина которого равна нулю, называют нулевым вектором и обозначают 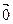 . Нулевой вектор направления не имеет.
. Нулевой вектор направления не имеет.
Вектор, длина которого равна единице, называют единичным вектором и обозначают 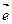 .
.
Единичный вектор, направление которого совпадает с направлением вектора  , называют ортом вектора
, называют ортом вектора  и обозначают
и обозначают 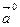 .
.
Векторы  и
и 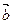 называют коллинеарными, если они лежат на одной прямой или на параллельных прямых; записывают
называют коллинеарными, если они лежат на одной прямой или на параллельных прямых; записывают  ||
|| 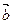 . Коллинеарные векторы могут быть направлены одинаково или противоположно. Нулевой вектор считается коллинеарным любому вектору.
. Коллинеарные векторы могут быть направлены одинаково или противоположно. Нулевой вектор считается коллинеарным любому вектору.

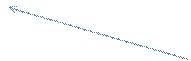
Два вектора  и
и 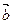 называют равными (
называют равными ( =
= 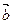 ), если они коллинеарны, одинаково направлены и имеют одинаковые длины.
), если они коллинеарны, одинаково направлены и имеют одинаковые длины.
Из определения равенства векторов следует, что вектор можно переносить параллельно самому себе, а начало вектора помещать в любую точку О пространства.
Равные векторы называют также свободными.
Три вектора в пространстве называют компланарными, если они лежат в одной плоскости или в параллельных плоскостях. Если среди трех векторов хотя бы один нулевой или два коллинеарны, то такие векторы компланарны.
2.
Под линейными операциями над векторами понимают операции сложения и вычитания векторов, а также умножение вектора на число.
Пусть  и
и 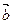 – два произвольных вектора. Возьмем произвольную точку О и построим вектор
– два произвольных вектора. Возьмем произвольную точку О и построим вектор 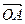 =
=  . От точки А отложим вектор
. От точки А отложим вектор 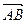 =
= 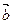 . Вектор
. Вектор 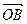 , соединяющий начало первого вектора с концом второго, называют суммой векторов
, соединяющий начало первого вектора с концом второго, называют суммой векторов  и
и 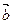 ; обозначают
; обозначают 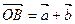 .
.
Это правило сложения векторов называют правилом треугольников.
Сумму двух векторов можно построить также по правилу параллелограмма.
Можно складывать несколько векторов, например, пусть требуется найти сумму векторов  ,
, 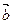 ,
, 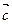 .
.
Возьмем произвольную точку О и построим вектор 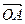 =
=  . От точки А отложим вектор
. От точки А отложим вектор 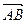 =
= 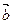 . От точки В отложим вектор
. От точки В отложим вектор 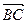 =
= 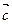 . Вектор
. Вектор 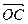 , соединяющий начало первого вектора с концом третьего, называют суммой векторов
, соединяющий начало первого вектора с концом третьего, называют суммой векторов  ,
, 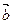 и
и 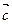 ; обозначают
; обозначают 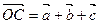 .
.
Под разностью векторов  и
и 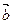 понимают вектор
понимают вектор 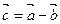 такой, что
такой, что 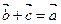 . Начало вектора
. Начало вектора 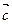 =
= 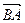 совпадает с концом В вектора
совпадает с концом В вектора 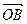 =
= 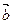 , а конец – совпадает с концом вектора
, а конец – совпадает с концом вектора 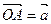 .
.
В параллелограмме, построенном на векторах  и
и 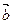 , одна направленная диагональ является суммой векторов
, одна направленная диагональ является суммой векторов  и
и 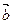 , а другая – разностью
, а другая – разностью  и
и 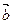 .
.
Можно вычитать векторы по правилу: 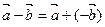 . Т.е. вычитание векторов заменить сложением вектора
. Т.е. вычитание векторов заменить сложением вектора  с вектором, противоположным вектору
с вектором, противоположным вектору 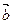 .
.
Произведением вектора  на скаляр (число) λ называют вектор λ·
на скаляр (число) λ называют вектор λ·  (или
(или  ·λ), который имеет длину |λ|·|
·λ), который имеет длину |λ|·|  |, коллинеарен вектору
|, коллинеарен вектору  , имеет направление вектора
, имеет направление вектора  , если λ > 0, и противоположное направление, если λ < 0. Например, если дан вектор
, если λ > 0, и противоположное направление, если λ < 0. Например, если дан вектор  , то векторы 3
, то векторы 3  и -2
и -2  будут иметь вид
будут иметь вид
Из определения произведения вектора на число следуют свойства этого произведения:
1) если 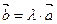 , то
, то 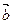 ||
||  . Наоборот, если
. Наоборот, если 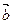 ||
||  , (
, ( ≠ 0), то при некотором λ верно равенство
≠ 0), то при некотором λ верно равенство 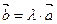 ;
;
2) всегда 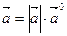 , т.е. каждый вектор равен произведению его модуля на орт.
, т.е. каждый вектор равен произведению его модуля на орт.
Линейные операции над векторами обладают следующими свойства ми:
1. 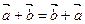 ,
,
2. 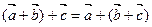 ,
,
3. 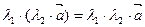 ,
,
4. 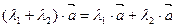 ,
,
5. 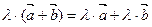 .
.
Эти свойства позволяют проводить преобразования в линейных операциях с векторами так, как это делается в обычной алгебре: слагаемые менять местами, вводить скобки, группировать, выносить за скобки как скалярные, так и векторные общие множители.
3.
Пусть в пространстве задана ось l, т.е. направленная прямая.
Проекцией точки М на ось l называют основание 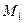 перпендикуляра
перпендикуляра 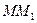 , опущенного из точки на ось.
, опущенного из точки на ось.
Если точка лежит на оси l, то проекция точки М на ось совпадает с М.
Пусть 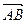 – произвольный вектор (
– произвольный вектор (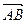 ≠
≠ 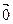 ). Обозначим через
). Обозначим через 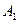 и
и 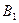 проекции на ось l соответственно начала А и конца В вектора
проекции на ось l соответственно начала А и конца В вектора 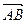 и рассмотрим вектор
и рассмотрим вектор 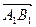 .
.
Проекцией вектора 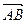 на ось l называют положительное число
на ось l называют положительное число 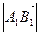 , если вектор
, если вектор 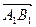 и ось l одинаково направлены и отрицательное число -
и ось l одинаково направлены и отрицательное число - 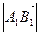 , если вектор
, если вектор 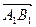 и ось l противоположно направлены. Если точки
и ось l противоположно направлены. Если точки 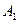 и
и 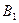 совпадают, то проекция вектора
совпадают, то проекция вектора 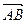 равна 0.
равна 0.
Углом φ между вектором и осью (или угол между двумя векторами) называют угол между двумя направлениями. Очевидно, что 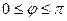 .
.
Основные свойства проекций:
1. Проекция вектора  на ось l равна произведению модуля вектора
на ось l равна произведению модуля вектора  на косинус угла φ между вектором и осью.
на косинус угла φ между вектором и осью.
2. Проекция вектора на ось положительна (отрицательна), если вектор образует с осью острый (тупой) угол, и равна нулю, если этот угол прямой.
3. Проекции равных векторов на одну и ту же ось равны между собой.
4. Проекция суммы нескольких векторов на одну и ту же ось равна сумме их проекций на эту ось.
5. При умножении вектора  на число λ его проекция на ось также умножается на это число.
на число λ его проекция на ось также умножается на это число.
Таким образом линейные операции над векторами приводят к соответствующим линейным операциям над проекциями этих векторов.
4.
Рассмотрим в пространстве прямоугольную систему координат Оxyz. Выделим на координатных осях Ox, Oy и Oz единичные векторы (орты),обозначаемые 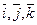 соответственно.
соответственно.
Выберем произвольный вектор  пространства и совместим его начало с началом координат:
пространства и совместим его начало с началом координат:  =
=  . Проведем через конец вектора
. Проведем через конец вектора 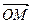 плоскости, параллельные координатным плоскостям. Точки пересечения этих плоскостей с осями обозначим соответственно через
плоскости, параллельные координатным плоскостям. Точки пересечения этих плоскостей с осями обозначим соответственно через 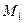 ,
, 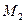 и
и 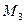 . Получим прямоугольный параллелепипед, одной из диагоналей которого является вектор
. Получим прямоугольный параллелепипед, одной из диагоналей которого является вектор 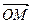 . По правилу параллелепипеда
. По правилу параллелепипеда 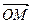 =
= 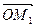 +
+ 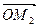 +
+ 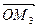 (*)
(*)
Поскольку 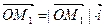 ,
, 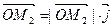 ,
, 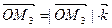 ;
;
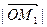 – проекция вектора
– проекция вектора 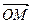 на ось Ох, обозначим ее
на ось Ох, обозначим ее 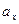 ,
, 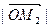 – проекция вектора
– проекция вектора 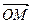 на ось Оy, обозначим ее
на ось Оy, обозначим ее 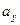 ,
, 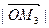 – проекция вектора
– проекция вектора 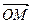 на ось Оz, обозначим ее
на ось Оz, обозначим ее 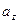 . Тогда формула (*) имеет вид:
. Тогда формула (*) имеет вид:
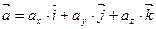 (**)
(**)
Эта формула является основной в векторном исчислении и называют разложением вектора по ортам координатных осей.
Числа 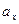 ,
, 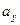 и
и 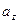 называют координатами вектора
называют координатами вектора  , т.е. координаты вектора есть его проекции на соответствующие координатные оси.
, т.е. координаты вектора есть его проекции на соответствующие координатные оси.
Векторное равенство (**) часто записывают в символическом виде 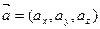 .
.
Равенство 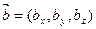 означает, что
означает, что 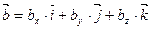 .
.
5.
Зная проекции вектора  на основании теоремы о длине диагонали прямоугольного параллелепипеда, можно найти выражение для модуля вектора:
на основании теоремы о длине диагонали прямоугольного параллелепипеда, можно найти выражение для модуля вектора: 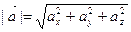 , т.е. модуль вектора равен квадратному корню из суммы квадратов его координат.
, т.е. модуль вектора равен квадратному корню из суммы квадратов его координат.
Пусть даны векторы 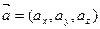 и
и 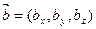 .
.
Так как линейные операции над векторами сводятся к соответствующим линейным операциям над проекциями этих векторов (над координатами), то можно записать:
1. 
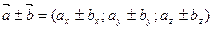 . То есть при сложении (вычитании) векторов их одноименные координаты складываются (вычитаются).
. То есть при сложении (вычитании) векторов их одноименные координаты складываются (вычитаются).
2. 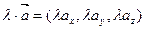 . То есть при умножении вектора на скаляр координаты вектора умножаются на этот скаляр.
. То есть при умножении вектора на скаляр координаты вектора умножаются на этот скаляр.
Из определения вектора как направленного отрезка, который можно передвигать в пространстве параллельно самому себе, следует, что два вектора равны тогда и только тогда, когда их одноименные координаты равны, т.е.
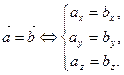
Если векторы заданы своими координатами, то векторы коллинеарны тогда и только тогда, когда их координаты пропорциональны.
Если в пространстве задана прямоугольная декартова система координат Oxyz и произвольная точка М, то координаты вектора  называют координатами точки М. Вектор
называют координатами точки М. Вектор  называют радиус-ветором точки М и обозначают
называют радиус-ветором точки М и обозначают 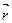 , т.е.
, т.е. 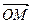 =
= 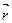 . Следовательно, координаты точки – это координаты ее радиус-вектора.
. Следовательно, координаты точки – это координаты ее радиус-вектора.
Пусть даны точки 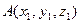 и
и 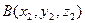 . Зная, что координаты точки это координаты вектора и что
. Зная, что координаты точки это координаты вектора и что 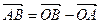 , получаем
, получаем 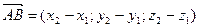 , т.е. координаты вектора равны разностям соответствующих координат его конца и начала.
, т.е. координаты вектора равны разностям соответствующих координат его конца и начала.
Скалярным произведением двух ненулевых векторов  и
и 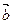 называют число, равное произведению длин этих векторов на косинус угла между ними.
называют число, равное произведению длин этих векторов на косинус угла между ними.
Свойства скалярного произведения векторов:
1. 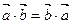 ,
,
2. 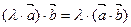 ,
,
3. 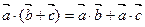 ,
,
4. 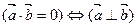 , т.е. скалярное произведение двух ненулевых векторов равно нулю тогда и только тогда, когда векторы перпендикулярны.
, т.е. скалярное произведение двух ненулевых векторов равно нулю тогда и только тогда, когда векторы перпендикулярны.
5. 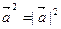 , т. е. скалярный квадрат вектора равен квадрату его длины.
, т. е. скалярный квадрат вектора равен квадрату его длины.
В частности: 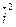 =
= 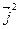 =
= 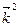 = 1.
= 1.
Если векторы заданы своими координатами, то скалярное произведение векторов равно сумме произведений их одноименных координат. То есть 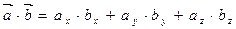 .
.
Определения угла между ненулевыми векторами 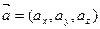 и
и 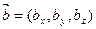 :
:
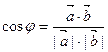 , т. е.
, т. е. 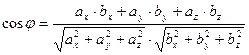 .
.
Отсюда следует условие перпендикулярности ненулевых векторов  и
и 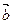 :
:
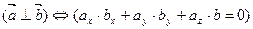 .
.

 2015-06-28
2015-06-28 2239
2239