Определение 1. Осью  называется прямая
называется прямая  с выбранным на ней направлением.
с выбранным на ней направлением.
Определение 2. Геометрической проекцией вектора 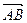 называется вектор
называется вектор 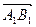 , где
, где 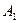 и
и 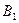 – ортогональные проекции точек А и В на ось
– ортогональные проекции точек А и В на ось 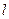 .
.
| рис. 2.18 |
Определение 3 Алгебраической проекцией вектора 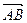 на ось
на ось 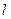 называется число, равное длине
называется число, равное длине 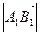 , взятое со знаком “
, взятое со знаком “ 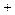 ”, если
”, если 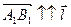 , и со знаком “-”, если
, и со знаком “-”, если 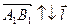 . Обозначается Пр l
. Обозначается Пр l 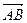 .
.
Теорема1. 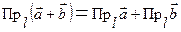 .
.
Доказательство:
Так как 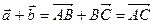 , то
, то 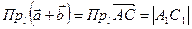 . С другой стороны,
. С другой стороны, 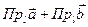 =
= 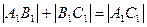 . ■
. ■
Теорема 2. 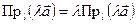 .
.
Доказательство:
Пусть 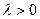 . Перенесём вектор
. Перенесём вектор  так, что его начало находилось на прямой
так, что его начало находилось на прямой 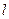 . Тогда треугольники
. Тогда треугольники 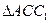 и
и 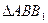 подобны. Если
подобны. Если 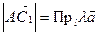 , а
, а 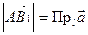 , то
, то 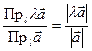 . Отсюда
. Отсюда 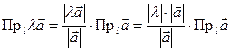 .
. 
| рис. 2.20 |
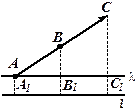 Так как
Так как 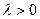 , то
, то 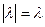 . Значит,
. Значит, 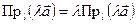 .
.
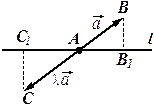 Если же
Если же 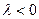 , то треугольники
, то треугольники 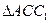 и
и 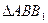 так же подобны. Но
так же подобны. Но 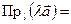
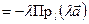 . ■
. ■
| рис. 2.21 |
Теорема 3. 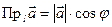 , где
, где 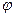 – угол между вектором
– угол между вектором  и положительным направлением оси
и положительным направлением оси 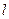 .
.
Доказательство:
| рис. 2.22 |
1. Угол 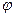 – острый, тогда очевидно, что
– острый, тогда очевидно, что 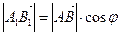 , т.е.
, т.е. 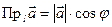 .
.
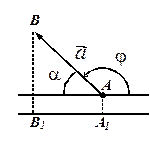 2. Угол
2. Угол 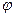 – тупой. Так как
– тупой. Так как 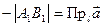 ,
, 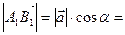
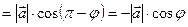 , то
, то 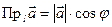 . ■
. ■
 2015-06-28
2015-06-28 429
429








