Цилиндрические поверхности

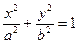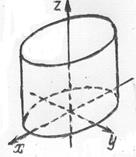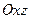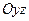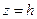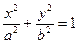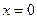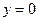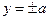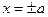6. Эллиптический цилиндр: . Как видно из уравнения, плоскости и являются плоскостями симметрии данного цилиндра. Сечение поверхности плоскостью представляет собой эллипс . Сечения цилиндра плоскостями и являются парами параллельных прямых и соответственно.

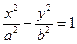7. Гиперболический цилиндр: .

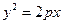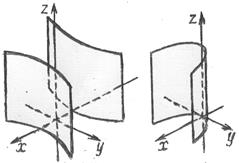
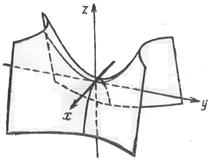9. Гиперболический параболоид

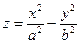. Из уравнения вытекает, что плоскост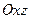и и 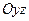являются плоскостями симметрии. Ось 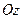называется осью гиперболического параболоида с плоскостью 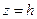представляет собой гиперболы 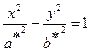, с полуосям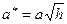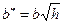и , при 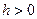, а при 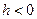– сопряжённые гиперболы для гипербол 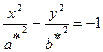с полуосями , .

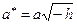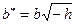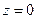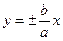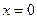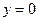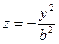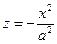Заметим, что плоскость пересекает поверхность по двум прямым , являющихся асимптотами вышеуказанных гипербол. Сечения плоскостями и являются параболами и соответственно.