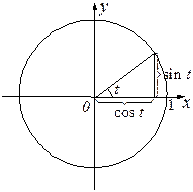2015-06-28
472
Тригонометрические функци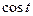и 
и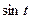 
определяются таким образом, что 
, 
, 
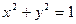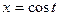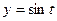, т.е. 
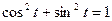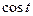. ( – абсцисса точки 
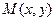на единичной окружности, 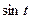– её ордината).
| рис.2.50 |
Если рассмотреть равнобочную гиперболу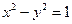 
, то можно ввести гиперболические функции 
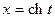(гиперболический косинус) и 
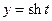(гиперболический синус) так, что 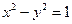, т.е. 
.
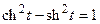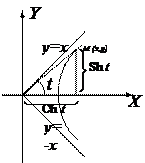Введём представление о числе 
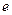. Рассмотрим все возможные функции 
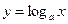и выберем из них ту, у которой касательная, проведённая через точку 
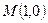, составляет угол 
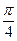с осью 
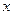. Основание такой логарифмической функции и есть число 
…
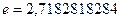Покажем, что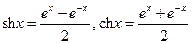 
.
Функция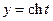 
– чётная, 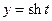– нечётная функция. Подставим 
, 
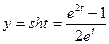в уравнении гиперболы. Получим
; 
; 
; 
.
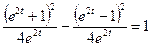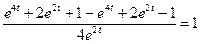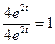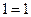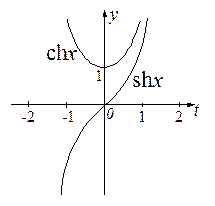Графики гиперболических функций:
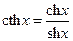- котангенс гиперболический.
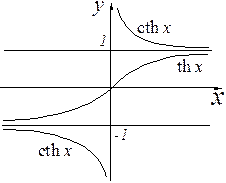
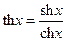- тангенс гиперболический.
