Функции

Если каждому элементу множества A поставлен в соответствии единственный элемент множества B, то говорят, что задано отображение из A в B или функция 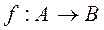. Если 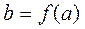, то элемент a называется образом элемента b, а b -прообразом элемента a.

Функция f называется:

- инъекцией, если из 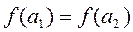следует ;

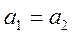- сюръекцией, если для каждого 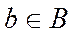существует 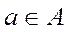такой, что ;

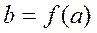- биекцией, если f является инъекцией и сюръекцией одновременно.

Для биекции f можно определить обратную функцию 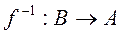. Примерами прямой и обратной функций в математическом анализе является 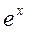и ln x, sin x и arcsin x, x² и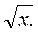

Если на множествах A и B определены отношения частичного порядка, то функция 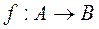называется монотонной, если из 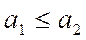следует .

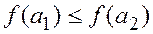Пусть 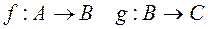. Тогда можно определить композицию функций g ● 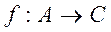, при которой образом элемента 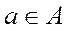является 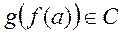. В курсе математического анализа подобную функцию называют сложной функцией.

Множество всех биекций из A в A с операцией композиции образует группу. Если A -конечное n -элементное множество, то это S_n -симметрическая группа степени n.