Соответствие между множествами А и В – это множество, представляющее собой некоторое подмножество их декартова произведения
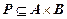 .
.
Полное соответствие между множествами А и В – это множество, равное их декартовому произведению
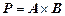 .
.
Если 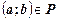 то говорят, что
то говорят, что 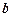 соответствует
соответствует 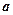 в соответствии
в соответствии 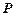 , ( или они находятся в соответствии Р).Обозначается:
, ( или они находятся в соответствии Р).Обозначается: 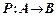 или
или 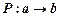 ,
, 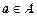 ,
, 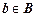 .
.
Соответствие предполагает, что некоторым элементам множества A (возможно, всем) поставлены в соответствие некоторые элементы множества B.
Соответствие, как и декартово произведение, можно изобразить графически в виде решетки или в виде векторной диаграммы. В узлах решетки оказываются соответствующие пары элементов декартова произведения.
Пусть имеются множества 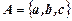 и
и 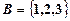 . Декартово произведение будет представлять собой следующую последовательность
. Декартово произведение будет представлять собой следующую последовательность
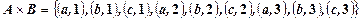 .
.
Из нее можно взять любые компоненты, которые и будут представлять собой соответствие из А в В, например
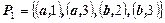 ,
, 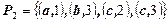 ,
, 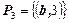 .
.
График соответствия для данных множеств представлен на рис. 2.2.
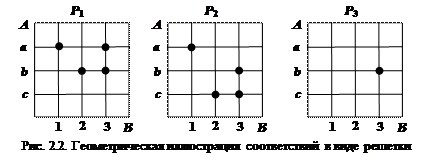
В виде векторной диаграммы соответствия представлены на рис. 2.3.

Образ элемента 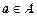 в множестве
в множестве 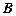 при соответствии
при соответствии 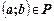 – множество всех
– множество всех 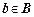 , соответствующих элементу
, соответствующих элементу 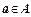 . Обозначается
. Обозначается 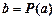 .
.
Прообраз элемента 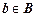 в множестве
в множестве 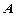 при соответствии
при соответствии 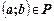 – множество всех
– множество всех 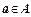 , соответствующих элементу
, соответствующих элементу 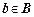 . Обозначается
. Обозначается 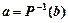 . Таким образом, если
. Таким образом, если 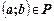 , то
, то 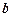 образ
образ 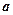 , а
, а 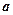 – прообраз
– прообраз 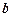 .
.
Область определения соответствия Р (обозначается 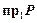 или
или 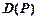 ) – множество таких
) – множество таких 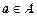 , для которых существует образ.
, для которых существует образ.
Область значений соответствия Р (обозначается 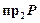 или
или 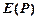 ) – множество таких
) – множество таких 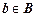 , для которых существует прообраз.
, для которых существует прообраз.
Всюду определенное соответствие – соответствие, при котором выполняется равенство 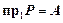 . В противном случае соответствие называется частичным.
. В противном случае соответствие называется частичным.
Сюръективное соответствие (сюръекция) – соответствие, при котором выполняется равенство 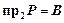 .
.
Инъективное соответствие (инъекция) – соответствие 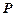 , при котором прообразом любого элемента из множества
, при котором прообразом любого элемента из множества 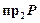 является единственный элемент из множества
является единственный элемент из множества 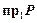 (соответствие не содержит пар с одинаковыми вторыми и различными первыми координатами).
(соответствие не содержит пар с одинаковыми вторыми и различными первыми координатами).
Функциональное соответствие (функция) – соответствие 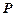 , при котором образом любого элемента из множества
, при котором образом любого элемента из множества 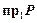 является единственный элемент из множества
является единственный элемент из множества 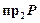 (соответствие не содержит пар с одинаковыми первыми и различными вторыми координатами).
(соответствие не содержит пар с одинаковыми первыми и различными вторыми координатами).
Взаимнооднозначное соответствие – соответствие, которое функционально и инъективно, то есть 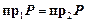 или
или 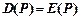 .
.
Биекция (1-1 соответствие) – соответствие, которое всюду определено, сюръективно, функционально и инъективно.
Отображение 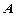 в
в 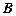 – соответствие, которое всюду определено и функционально.
– соответствие, которое всюду определено и функционально.
Отображение 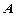 на
на 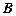 – соответствие, которое всюду определено, функционально и сюръективно.
– соответствие, которое всюду определено, функционально и сюръективно.
Равномощные множества – множества, между которыми можно установить биекцию.
Счетное множество – множество, равномощное множеству натуральных чисел.
Континуальное множество – множество, равномощное множеству действительных чисел отрезка 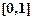 .
.
 2015-06-28
2015-06-28 2842
2842
