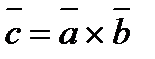 ,
,
1) модуль 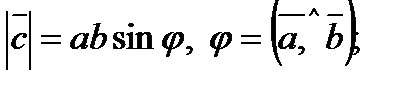
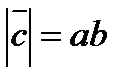 , коли
, коли 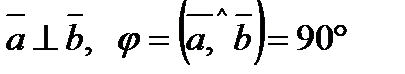
2) вектор 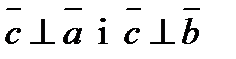 ;
;
3) напрям вектора 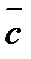 такий, щo …
такий, щo …
Геометричні властивості векторного добутку.
1. 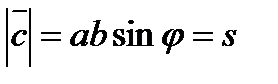
2. 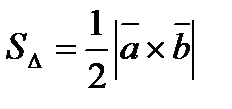 .
.
3. 
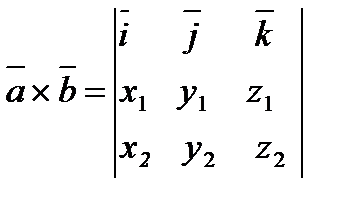 ,
,
Приклади.
1) Знайти площу трикутника з вершинами А(4, -1, 2), В(-8, 0, 4), С(8, 2, 3).
Розв¢язання.
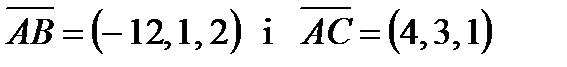 .
.
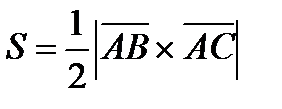 .
.
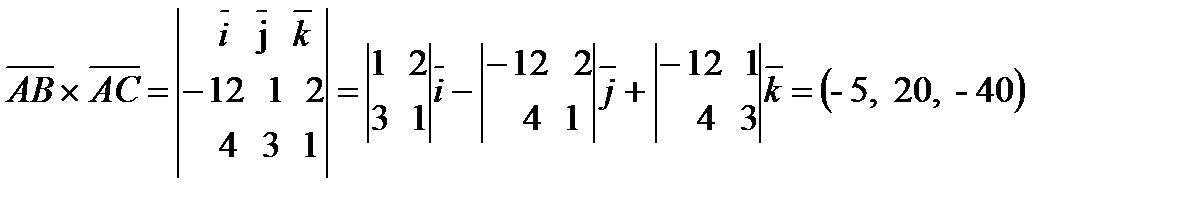 .
.
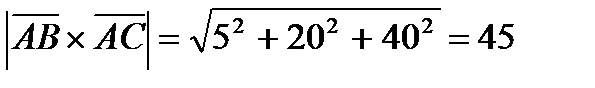 .
. 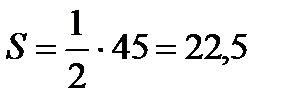 .
.
Мішаний (векторно-скалярний) добуток трьох векторів.
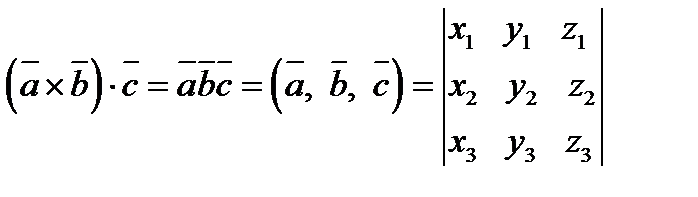
Об’єм паралелепіпеда:
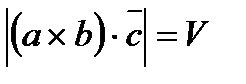 .
.
Об’єм піраміди:
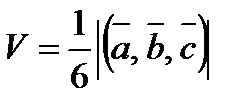
2) Обчислити висоту паралелепіпеда, побудованого на векторах 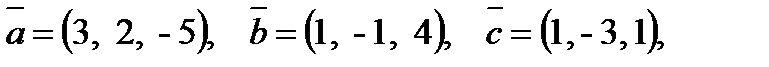 якщо в основі його лежать вектори
якщо в основі його лежать вектори 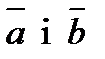 .
.
Розв¢язання. 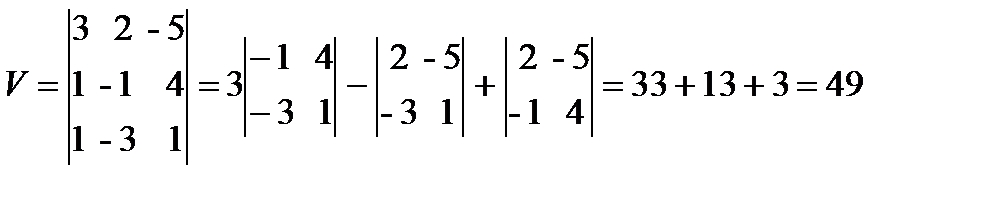 .
. 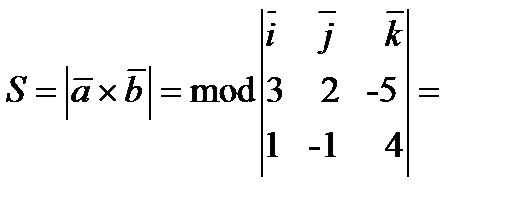
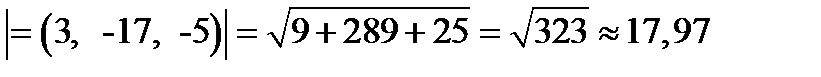
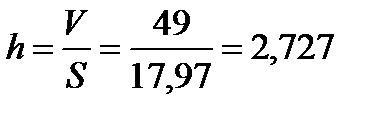 .
.
5) Знайти висоту Н трикутної піраміди, опущеної з вершини О, якщо її вершини А(3, 2, 1), В(4, 0, -1), С(2, -1, 0) і D(4, 2, 5).
Розв¢язання. 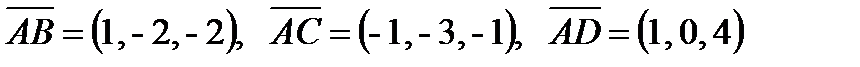
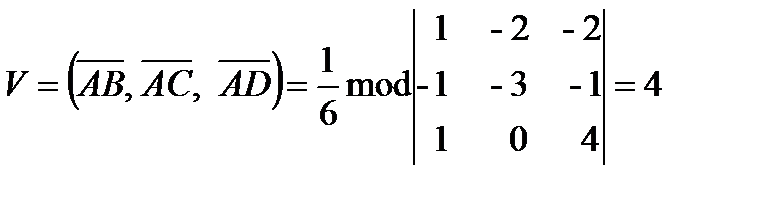 .
.
Знаходимо площу S основи АВС:
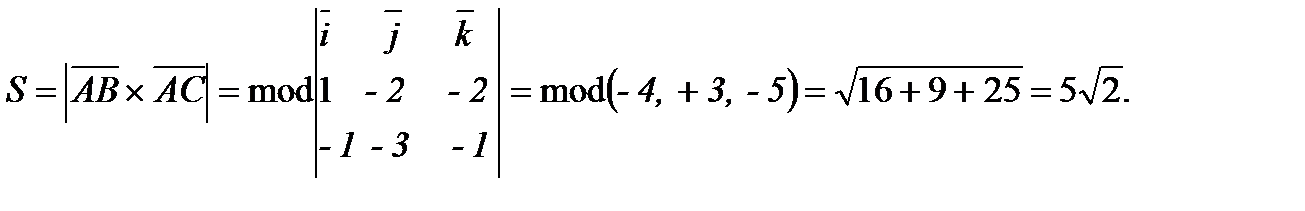
Висота піраміди:
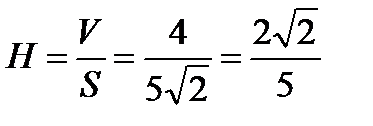 .
.
 2015-06-28
2015-06-28 823
823








