Вектори і дії над ними
1) 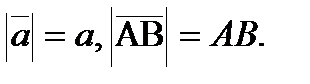
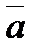 |
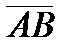 |
| А |
| В |
2). 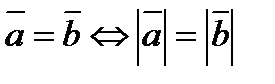 ,
, 
 |
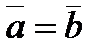 |
 |
3). 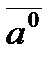 ;
; 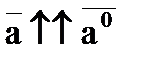 ,
, 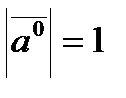 ,
, 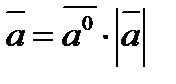
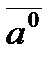
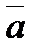
4). 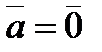 ,
,  ,
,
5).
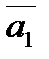 |
 |
 |
| В |
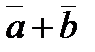  |
| А |
| С |
| В |
| О |
| А |
| С |
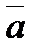 |
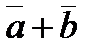 |
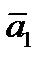 |
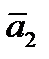 |
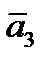 |
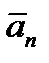 |
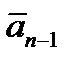 |
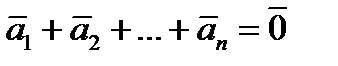 |
6). Закони додавання:
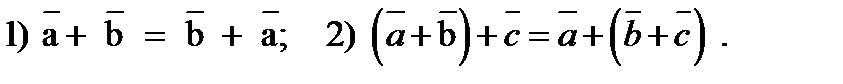
Протилежні вектори:
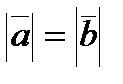 ,
, 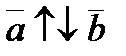 ,
, 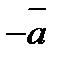 ,
, 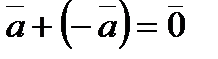 .
.
Віднімання векторів:
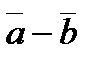 :
: 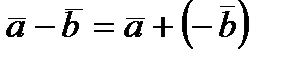
| О |
Множення вектора на скаляр.
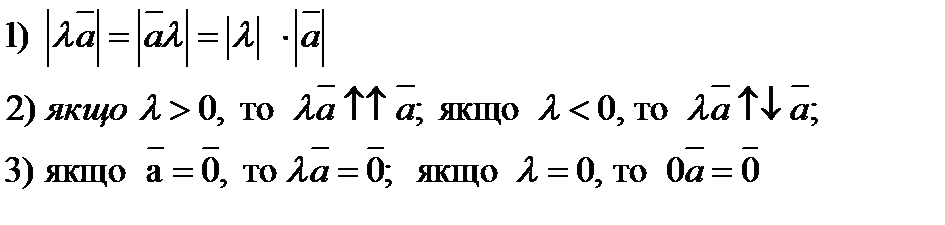
Закони множення вектора на скаляр:

8). Колінеарні вектори.
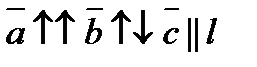 ,
,
9). Компланарні вектори.
Розклад вектора по трьом не компланарним векторам
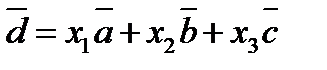 ,
,
Ортогональний базис
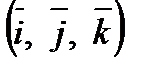 ,
, 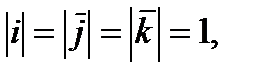
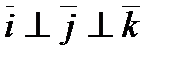 ,
,
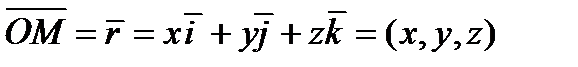
| Z |
| 0 |
| X |
| У |
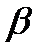 |
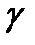 |
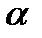 |
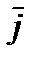 |
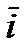 |
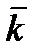 |
| А(x,o,o) |
| С(о,о,z) |
| М |
| В(o,y,o) |
. 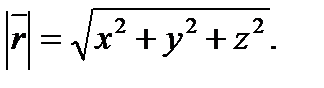
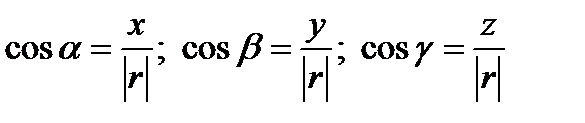
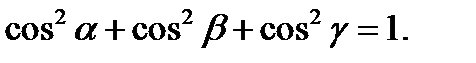
Лінійні операції над векторами в координатній формі.
1. 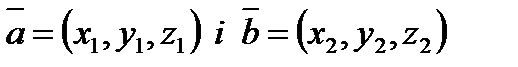 .
. 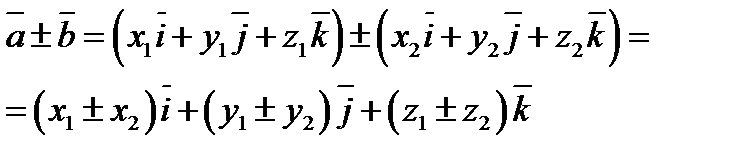
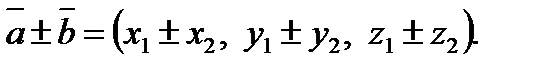
2. 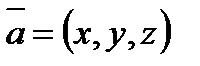 ,
, 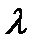
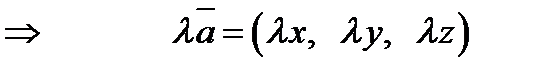
3. 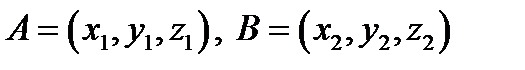
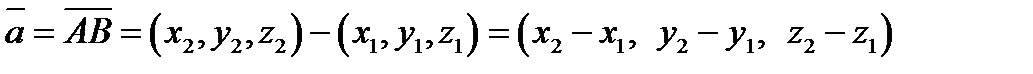
4. 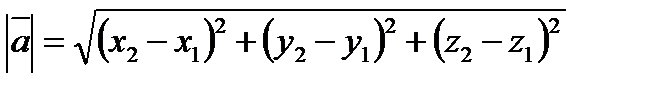
5. Поділ відрізка в заданому відношенні: 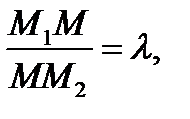
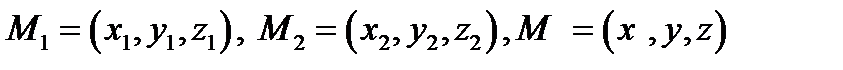
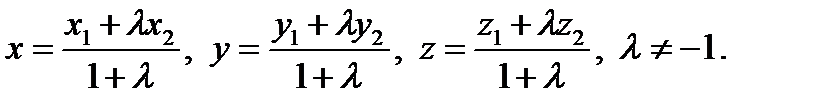
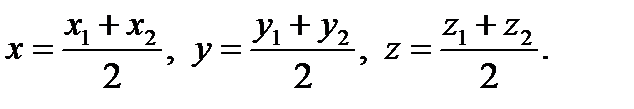
Скалярний добуток двох векторів.
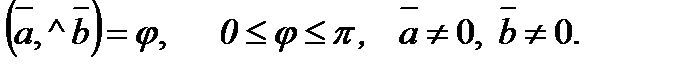
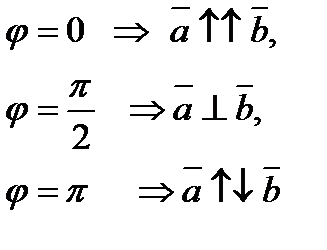
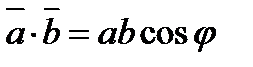
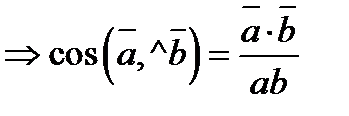
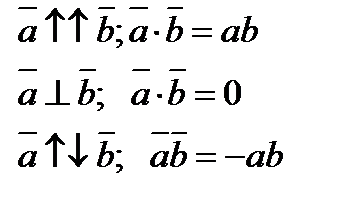
Проекція вектора на вектор

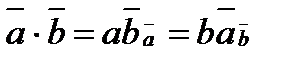
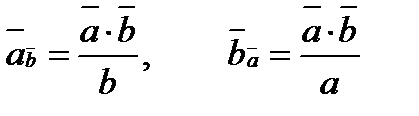
Закони скалярного добутку:
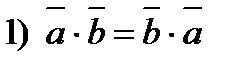 - переставний,
- переставний,
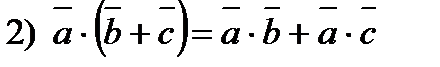 - розподільчий,
- розподільчий,
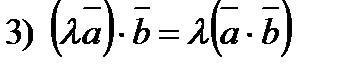 - сполучний
- сполучний
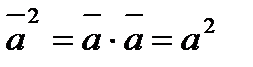
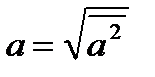
Таблиця скалярного добутку ортів:
· 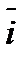
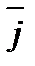
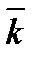
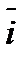 1 0 0
1 0 0
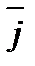 0 1 0
0 1 0
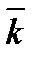 0 0 1
0 0 1
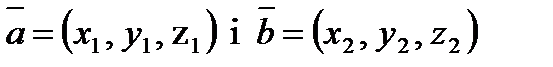 .
.
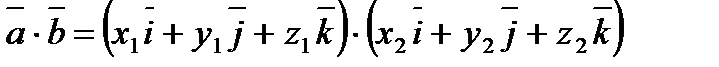
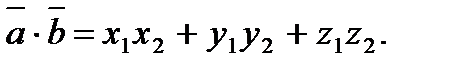
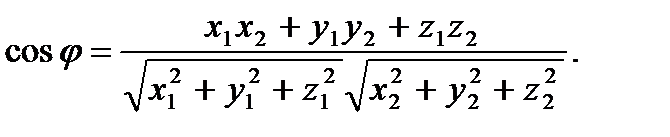
Приклади:
1) Задано точки А(3, 1, 0), В(0, -2, 6), С(3, -2, 0) і D(1, -2, 4). Обчислити проекцію 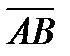 на
на 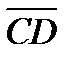 .
.
Розв ¢язання. 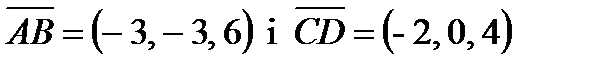 .
.
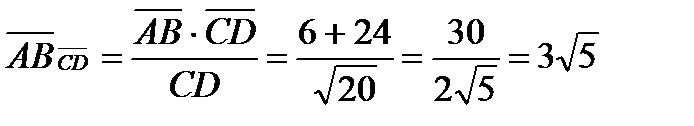 .
.
2) Знайти модуль вектора
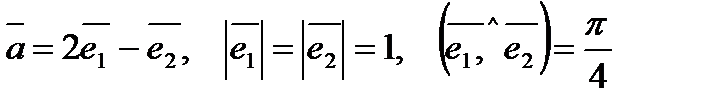
Розв¢язання.
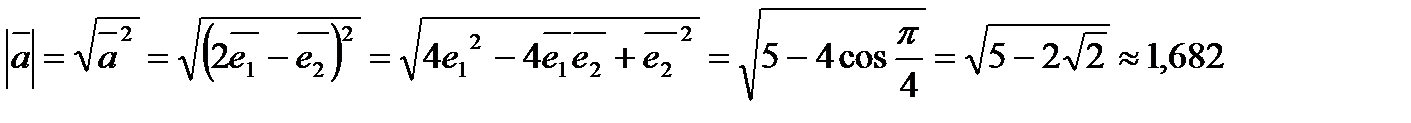 .
.
3) Обчислити довжину діагоналей паралелограма ABCD, якщо
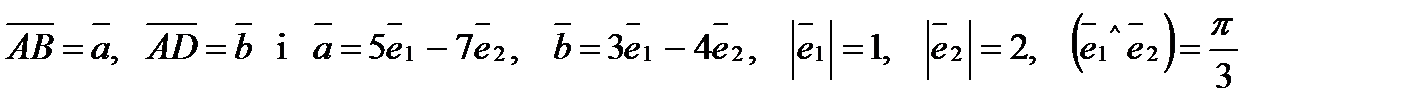
Розв¢язання.

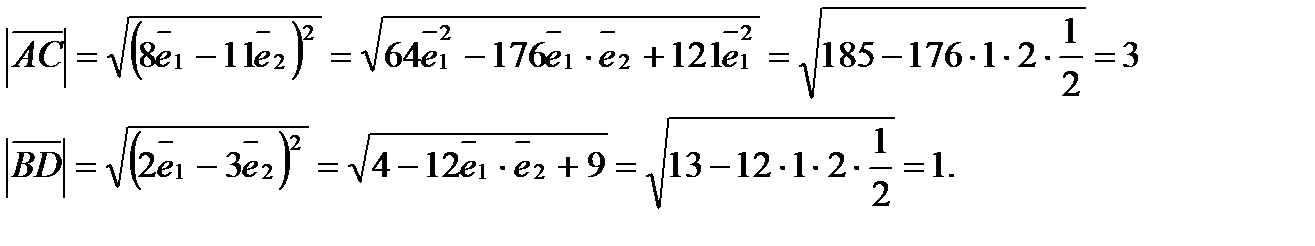
4) Обчислити: 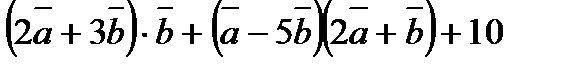 , якщо
, якщо 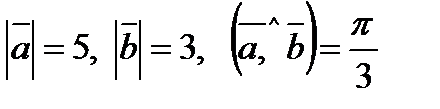 .
.
Розв¢язання.
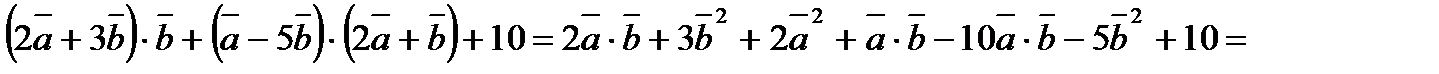
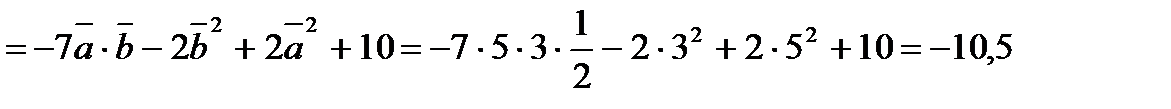
 2015-06-28
2015-06-28 897
897








