Он ищется в виде
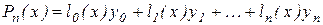 (2.2) (2.2)
|
где коэффициенты 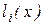 являются многочленами и удовлетворяют условиям
являются многочленами и удовлетворяют условиям
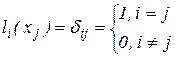 .
.
Оказывается, что этих требований достаточно для однозначного определения 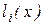 . Действительно, многочлен
. Действительно, многочлен 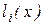 обращается в ноль в узловых точках
обращается в ноль в узловых точках 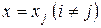 . Следовательно, он имеет разложение
. Следовательно, он имеет разложение
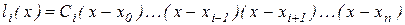 .
.
Положим теперь 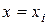 . Тогда
. Тогда
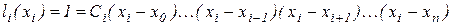 ,
,
откуда
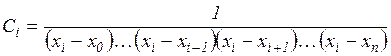 .
.
С целью сокращения записи введем функцию
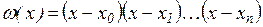 , (2.3) , (2.3)
|
тогда
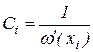 ,
,
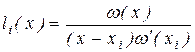
и многочлен (2.2) принимает вид
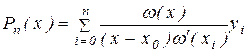 , (2.4) , (2.4)
|
где ω(x) описывается выражением (2.3). Многочлен (2.4) и называется интерполяционным многочленом Лагранжа.
 2015-06-24
2015-06-24 652
652








