По аналогии с (2.6) рассмотрим многочлен степени n.
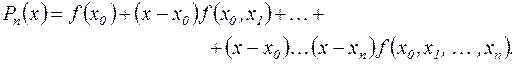 (2.7) (2.7)
|
Определим его значения в узловых точках. Так, непосредственно из (2.7) имеем
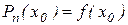
Далее,
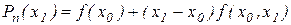 ,
,
но, с учетом (2.6) при 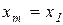 это равняется
это равняется 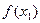 .
.
Т.о.
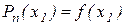
Аналогичным образом получаем, что
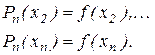
Таким образом, многочлен (2.7) принимает заданные значения в заданных точках и, следовательно, является интерполяционным. Он и называется интерполяционным многочленом Ньютона. Заметим, что в силу единственности (п. 2.2) различия между интерполяционными многочленами Лагранжа и Ньютона чисто внешние.
 2015-06-24
2015-06-24 661
661








