Определение [3.1]. Аксиома 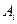 системы аксиом
системы аксиом 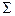 ={
={ 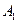 ,
, 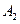 ,
, 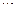 ,
, 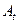 } называется зависимой от остальных аксиом системы
} называется зависимой от остальных аксиом системы 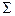 , если предложение
, если предложение 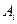 является логическим следствием из остальных аксиом системы
является логическим следствием из остальных аксиом системы 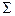 . В противном случае аксиома
. В противном случае аксиома 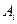 называется независимой от системы аксиом
называется независимой от системы аксиом 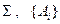 .
.
Теорема [3.1]. Пусть 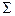 — непротиворечивая система аксиом. Если замена аксиомы
— непротиворечивая система аксиом. Если замена аксиомы 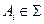 ее отрицанием
ее отрицанием 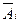 приводит снова к непротиворечивой системе аксиом
приводит снова к непротиворечивой системе аксиом 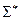 =(
=(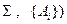
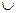
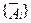 , то аксиома
, то аксиома 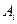 не зависит от остальных аксиом системы
не зависит от остальных аксиом системы 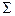 .
.
Определение [3.2]. Система аксиом 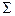 называется независимой, если каждая ее аксиома не зависит от остальных аксиом этой системы.
называется независимой, если каждая ее аксиома не зависит от остальных аксиом этой системы.
Из теоремы вытекает критерий независимости аксиомы: чтобы установить независимость аксиомы непротиворечивой системы аксиом 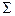 , надо заменить эту аксиому ее отрицанием и доказать с помощью построения модели непротиворечивость полученной системы аксиом
, надо заменить эту аксиому ее отрицанием и доказать с помощью построения модели непротиворечивость полученной системы аксиом 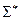 .
.
 2015-06-24
2015-06-24 1241
1241
