2015-06-24
1622
Пусть имеются некоторые множества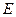 
, 
, 
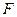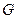и на этих множествах определены некоторые отношения 
, 
, 
, 
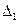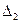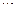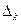, которые можно задать или как некоторые подмножества декартовых произведений множеств 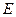, , 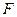, 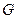или указав свойства 
, 
, , 
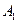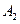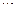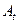(аксиомы), которыми они обладают.
В дальнейшем будем всегда задавать отношения 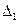, , 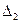, 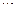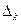аксиомами.
Может случиться, что указанными свойствами 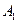, , 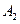, 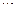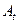обладает и другая система отношений 
, 
, , 
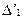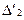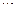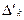. Например, на множестве действительных чисел 
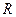алгебраические операции 
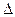— сложение и 
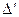— умножение обладают одним и тем же свойством коммутативности. Обозначим через 
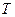множество всех систем отношений 
= { , , , }, 
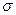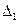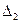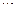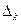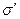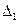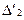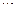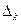= { , , , }, для которых выполняются аксиомы , , , .
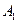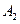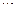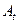Определение [1.1]. Говорят, что на множествах 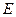, , 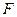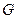задана математическая структура рода 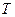, если задан элемент 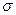непустого множества 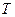с помощью аксиом 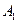, , 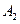, 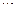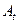; 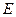, , 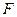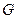— база структуры рода .
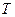Пример 1 (структура группы).
База — одно множество ;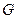
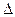— алгебраическая операция, заданная на 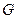и обладающая свойствами:
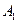— замкнутость;
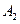— ассоциативность;
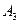— существование нейтрального элемента;
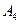— существование симметричного элемента.
Отношение 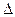определяет на множестве 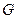структуру рода группы и тогда говорят короче: 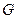— группа.
Пример 2 (структура векторного пространства).
База — два множества: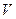 
и поле 
;
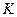Система отношений — ={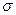 
, 
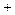}где
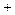(сложение): 
, 
;
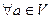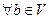
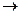
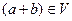(умножение): ,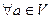 
;
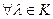
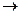
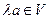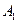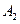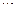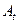, , , — известные свойства, которыми обладают отношения 
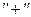и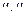 
.
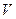называют векторным пространством над полем .
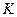Во втором примере множество 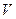играет основную роль, а множество 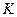является вспомогательным.
Совокупность всех утверждений, которые могут быть получены из аксиом математической структуры путем логического вывода, составляет теорию этой математической структуры. Таким образом, для построения математической теории необходимо:
1) указать некоторые основные множества (их элементы называют основными) и вспомогательные множества;
2) указать систему аксиом, которые задают отношения, называемые основными.
Этот метод построения математической теории называется аксиоматическим методом.
