Определим основные понятия "прямая", "плоскость"; основное отношение "лежит между", понятия: "луч", "полуплоскость" и др. и рассмотрим некоторые их свойства.
Прямая.
Определение [3.1]. Прямой с начальной точкой  и направляющим вектором
и направляющим вектором 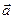
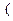
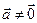 ) называется множество всех таких точек
) называется множество всех таких точек 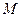 пространства
пространства 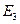 , что
, что 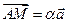 ,
, 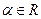 .
.
Из определения следует:
1) прямая имеет бесконечное множество точек;
2) любая точка прямой может быть взята за начальную;
3) в качестве направляющего вектора может быть взят любой другой ненулевой вектор, коллинеарный вектору 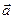 .
.
Теорема [3.1]. Через всякие две точки проходит одна и только одна прямая.
Плоскость.
Определение [3.2]. Плоскостью с начальной точкой  и направляющими векторами
и направляющими векторами 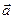 и
и 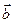 (
(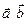 ) называется множество всех таких точек
) называется множество всех таких точек 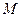 пространства
пространства 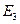 , что
, что 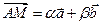 ,
, 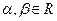 .
.
Плоскость обладает следующими свойствами:
1) плоскость имеет бесконечное множество точек;
2) любая точка плоскости может быть взята за начальную;
3) в качестве направляющих векторов плоскости можно взять любые два неколлинеарных вектора, которые являются линейными комбинациями векторов 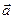 и
и 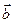 , т. е. принадлежат линейной оболочке, натянутой на векторы
, т. е. принадлежат линейной оболочке, натянутой на векторы 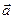 и
и 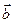 .
.
Теорема [3.2]. Через любые три неколлинеарные точки проходит одна и только одна плоскость.
Теорема [3.3]. Если две точки  и
и  прямой
прямой  принадлежат плоскости
принадлежат плоскости 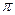 , то каждая точка прямой
, то каждая точка прямой  лежит в плоскости
лежит в плоскости 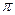 .
.
Отношение "лежит между".
Определение [3.3]. Будем говорить, что точка  лежит между точками
лежит между точками  и
и  , и обозначать
, и обозначать 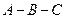 , если
, если 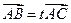 и
и 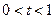 .
.
Рассмотрим некоторые свойства.
1. Если 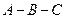 , то
, то  ,
,  ,
,  — три различные точки, лежащие на одной прямой.
— три различные точки, лежащие на одной прямой.
2. Если 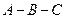 , то
, то 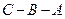 .
.
Понятия "отрезок", "луч".
Определение [3.4]. Отрезком 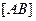 называется объединение точек
называется объединение точек  и
и  со множеством всех точек
со множеством всех точек 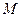 , лежащих между
, лежащих между  и
и  .
.
Таким образом, отрезок 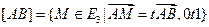 .
.
Определение [3.5]. Лучом 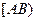 называется объединение отрезка
называется объединение отрезка 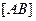 со множеством всех таких точек
со множеством всех таких точек 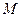 , что точка
, что точка  лежит между
лежит между  и
и 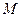 .
.
Очевидно, луч 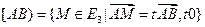 .
.
Если 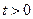 , то луч
, то луч 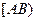 называется открытым.
называется открытым.
Теорема [3.4]. Пусть имеется прямая  и точка
и точка 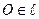 . Точка
. Точка 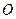 разбивает множество всех точек прямой
разбивает множество всех точек прямой  , отличных от точки
, отличных от точки 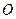 , на два непустых подмножества так, что:
, на два непустых подмножества так, что:
1) если две точки принадлежат одному и тому же подмножеству, то одна из них лежит между точкой 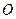 и другой точкой;
и другой точкой;
2) если две точки принадлежат различным подмножествам, то точка 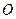 лежит между этими точками.
лежит между этими точками. 
Полуплоскость.
Определение [3.6]. Пусть имеется плоскость 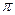 и прямая
и прямая  , принадлежащая этой плоскости. Будем говорить, что точки
, принадлежащая этой плоскости. Будем говорить, что точки  и
и  плоскости
плоскости 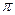 , отличные от точек прямой
, отличные от точек прямой  , лежат по одну сторону от прямой
, лежат по одну сторону от прямой  , если отрезок
, если отрезок 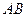 не пересекает прямую
не пересекает прямую  и лежат по разные стороны от прямой
и лежат по разные стороны от прямой  , если отрезок
, если отрезок 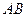 пересекает эту прямую.
пересекает эту прямую.
Теорема [3.5]. Пусть имеются плоскость 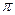 и прямая
и прямая 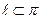 . Прямая
. Прямая  разбивает множество всех точек плоскости
разбивает множество всех точек плоскости 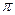 , не лежащих на прямой
, не лежащих на прямой  , на два непустых подмножества так, что:
, на два непустых подмножества так, что:
1) если две точки принадлежат одному подмножеству, то они лежат по одну сторону от прямой  ;
;
2) если две точки принадлежат различным подмножествам, то они лежат по разные стороны от прямой  .
.
Каждое из подмножеств 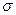 и
и 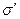 называется открытой полуплоскостью с границей
называется открытой полуплоскостью с границей  . Объединение открытой полуплоскости с ее границей называется полуплоскостью.
. Объединение открытой полуплоскости с ее границей называется полуплоскостью.
Таким образом, всякая прямая разбивает полуплоскость, в которой прямая лежит, на две полуплоскости.
Расстояние.
Определение [3.7]. Расстоянием 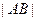 называется длина вектора
называется длина вектора 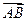 , т. е.
, т. е.
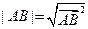 (3.9)
(3.9)
Теорема [3.6]. Расстояние обладает следующими свойствами:
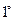 .
. 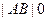 , при этом
, при этом 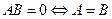 .
.
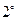 .
. 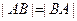 .
.
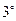 . (
. (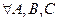 )
)  |AB|+|BC||AC|
|AB|+|BC||AC| 
Параллельность.
Определение [3.8]. Прямая  называется параллельной прямой
называется параллельной прямой 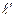 , если направляющий вектор прямой
, если направляющий вектор прямой  коллинеарен направляющему вектору прямой
коллинеарен направляющему вектору прямой 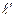 .
.
Так как коллинеарность векторов является отношением эквивалентности, то и параллельность прямых обладает свойствами рефлексивности, симметричности и транзитивности.
Обозначение: 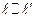 —
—  и
и 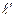 параллельные прямые.
параллельные прямые.
Теорема [3.7]. В плоскости через точку, не лежащую на данной прямой, проходит не более одной прямой, параллельной данной.
 2015-06-24
2015-06-24 1010
1010
