2015-06-24
1795
Зададим структуру трехмерного евклидова пространства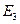 
или, короче, определим пространство 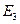следующим образом.
Определение [1.1]. Пусть имеется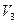 
— трехмерное векторное пространство, построенное над полем вещественных чисел 
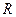и пусть 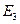— некоторое непустое множество.
Элементы пространства 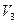обозначим 
, 
, 
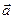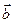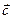, …и назовем векторами;
элементы поля 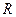— вещественные числа 
, 
, 
, …;
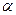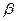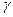элементы множества 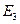— точки 
, 
, 
, ….
Тогда множество 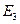называется трехмерным евклидовым пространством, если задано отображение 
: 
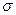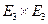
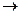
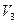, которое каждой паре точек 
, 
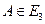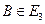ставит в соответствие единственный вектор 
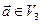, обозначаемый 
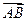, так, что выполняются следующие свойства:
, 
: 
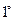
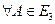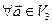
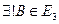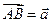(т. е. от любой точки можно отложить единственным образом вектор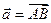 
).
Для любых трех точек , , выполняется равенство
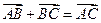(аксиома треугольника).
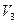Пространство — трехмерное евклидово векторное пространство, т. е. в пространстве 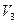задана билинейная форма, называемая скалярным произведением, которая каждой паре векторов 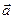, 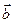ставит в соответствие число, обозначаемое 
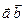и удовлетворяющее свойствам:
1) (
), (
) 
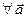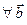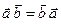(коммутативность),
2) (
), (), () 
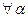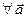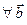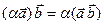(ассоциативность умножения на число),
3) (), (), (
) 
,
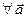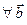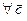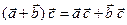4) скалярный квадрат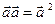 
является неотрицателеным числом, при этом 
.
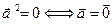Базой в структуре трехмерного евклидова пространства является точечное пространство 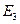. Векторное пространство 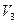называется пространством переносов евклидова пространства 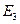, это вспомогательное множество.
Заметим, что для определения пространства переносов 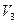надо, в свою очередь, задать:
— множество 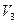и множество 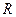вещественных чисел,
— отношения " сумма векторов " и " умножение вектора на число ",
— свойства, которым эти отношения удовлетворяют, т. е. аксиомы векторного пространства.
В свою очередь, поле 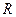вещественных чисел тоже определяется аксиоматически.
Таким образом, математическая структура трехмерного евклидова пространства довольно сложная, но мы полагаем, что математические теории трехмерного евклидова векторного пространства 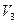и поля вещественных чисел 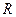построены.
Из всего сказанного следует, что основными отношениями, задающими структуру пространства 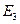, являются: 
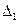— сложение векторов, 
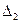— умножение вектора на число, 
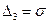— откладывание вектора, 
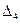— скалярное умножение. Аксиомы структуры 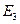— это свойства 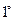, , 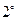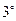в его определении. Система всех аксиом, лежащих в основе определения пространства 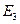, называется системой аксиом Вейля.
Теорема [1.1]. Система аксиом Вейля трехмерного евклидова пространства непротиворечива постольку, поскольку непротиворечива арифметика вещественных чисел.
