Непротиворечивость системы аксиом

Как уже отмечалось, чтобы построить какую либо математическую теорию надо выбрать множества и задать на них отношения, удовлетворяющие определенной системе аксиом. Очевидно, что аксиомы не могут быть выбраны произвольно, они должны подчиняться определенным требованиям. А именно, система аксиом должна быть:

1) непротиворечивой,

2) независимой,

3) полной.

Определение [2.1]. Система аксиом 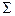={ 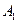, , 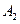, 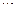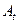} называется (внутренне) непротиворечивой, если из аксиом системы путем логического вывода нельзя вывести два взаимно исключающих друг друга утверждения ( и отрицание ).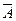

Задача доказательства внутренней непротиворечивости системы аксиом является по существу задачей математической логики и, в общем, установить внутреннюю непротиворечивость почти невозможно. Однако можно установить содержательную непротиворечивость системы аксиом.

Определение [2.2]. Говорят, что построена модель (интерпретация, реализация) математической структуры, если в качестве основных и вспомогательных множеств взяты конкретные множества и основным отношениям придан конкретный смысл так, что все аксиомы 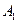, , 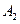, 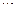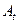оказываются выполненными.

Определение [2.3]. Система аксиом математической структуры называется содержательно непротиворечивой, если существует модель этой математической структуры.

Таким образом, чтобы доказать содержательную непротиворечивость системы аксиом математической структуры, надо выбрать конкретные множества и задать на них конкретные отношения так, чтобы выполнялись все аксиомы, т. е. придать конкретный смысл основным понятиям (элементам) и основным отношениям.