Полнота системы аксиом

Пусть имеется математическая структура, заданная с помощью системы аксиом ={ , , , }.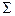

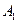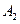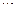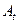Определение [4.1]. Система аксиом 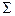называется неполной, если существует предложение , сформулированное в терминах теории структуры и удовлетворяющее следующим условиям:

а) оно не вводит новых отношений структуры;

б) не зависит от аксиом системы ;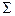

в) система аксиом 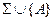непротиворечива.

Если такого предложения не существует, то система 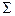называется полной.

Очевидно, что, пользуясь этим определением, невозможно установить, является ли исследуемая система аксиом полной или неполной. Существует, так называемый, критерий полноты.

Определение [4.2]. Пусть имеется математическая структура, заданная на множествах 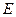, , 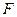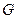с помощью отношений 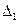, , 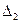, , 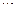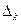удовлетворяющих системе аксиом 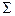={ 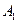, , 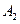, 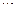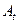}, и пусть построены две модел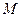и и 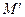этой математической структуры. Тогда эти модели называются изоморфными, если между ними можно установить биективное соответствие, сохраняющее структуру, т. е. соответствующие элементы находятся в одном и том же отношении .

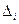Теорема [ 4.1]. Если все модели математической структуры, построенной с помощью непротиворечивой системы аксиом 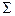, изоморфны, то система аксиом 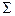полная.

Из теоремы следует критерий полноты: для того, чтобы установить полноту системы аксиом, надо доказать изоморфизм всех ее моделей.

Очевидно, что изоморфизм моделей одной и той же математической структуры является отношением эквивалентности. Поэтому для доказательства полноты системы аксиом достаточно фиксировать какую-либо одну модель и установить изоморфизм между произвольной моделью и этой фиксированной моделью.

Лекция № _ 2 __

Тема:_ СИСТЕМА АКСИОМ ВЕЙЛЯ ЕВКЛИДОВА ПРОСТРАНСТВА_

Основные вопросы, рассматриваемые на лекции:

Непротиворечивость и полнота системы аксиом Вейля. Определение простейших фигур. О связи систем аксиом Вейля и школьного курса.