По Гильберту, база структуры евклидова пространства состоит из трех множеств 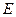 ,
, 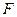 ,
, 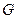 . Элементы множества
. Элементы множества 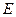 называются точками и обозначаются буквами
называются точками и обозначаются буквами  ,
,  ,
,  ,...; элементы множества
,...; элементы множества 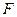 называются прямыми и обозначаются буквами
называются прямыми и обозначаются буквами 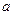 ,
, 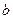 ,
, 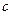 ,...; элементы множества
,...; элементы множества 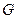 — плоскостями и обозначаются буквами
— плоскостями и обозначаются буквами 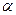 ,
, 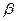 ,
, 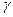 ,... Основными отношениями являются отношения, которые обозначаются словами: "принадлежит" (или "лежит на"), "лежит между" и "конгруэнтны".
,... Основными отношениями являются отношения, которые обозначаются словами: "принадлежит" (или "лежит на"), "лежит между" и "конгруэнтны".
Список аксиом содержит 20 аксиом, которые разбиты на пять групп.
I группа аксиом — аксиомы принадлежности.
I 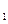 . Для любых двух точек
. Для любых двух точек  и
и  существует прямая, которой принадлежит каждая из них.
существует прямая, которой принадлежит каждая из них.
I 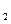 . Существует не более одной прямой, которой принадлежит каждая из двух данных точек
. Существует не более одной прямой, которой принадлежит каждая из двух данных точек  и
и  .
.
I 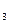 . На каждой прямой существуют по крайней мере две точки. Существуют по меньшей мере три точки, не принадлежащие одной прямой.
. На каждой прямой существуют по крайней мере две точки. Существуют по меньшей мере три точки, не принадлежащие одной прямой.
I 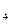 . Для любых трех точек
. Для любых трех точек  ,
,  ,
,  , не принадлежащих одной прямой, существует плоскость, которой принадлежит каждая из этих точек; каждой плоскости принадлежит по меньшей мере одна точка.
, не принадлежащих одной прямой, существует плоскость, которой принадлежит каждая из этих точек; каждой плоскости принадлежит по меньшей мере одна точка.
I 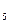 . Каковы бы ни были три точки
. Каковы бы ни были три точки  ,
,  ,
,  , не принадлежащие одной прямой, существует не более одной плоскости, которой принадлежит каждая из трех точек
, не принадлежащие одной прямой, существует не более одной плоскости, которой принадлежит каждая из трех точек  ,
,  ,
,  .
.
I 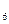 . Если две точки
. Если две точки  и
и  прямой
прямой 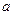 принадлежат плоскости
принадлежат плоскости 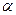 , то и каждая точка прямой
, то и каждая точка прямой 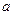 принадлежит плоскости
принадлежит плоскости 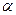 .
.
I 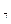 . Если две плоскости
. Если две плоскости 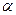 и
и 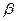 имеют общую точку
имеют общую точку  , то они имеют по меньшей мере еще одну общую точку
, то они имеют по меньшей мере еще одну общую точку  .
.
I 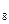 . Существуют по меньшей мере четыре точки, не принадлежащие одной плоскости.
. Существуют по меньшей мере четыре точки, не принадлежащие одной плоскости.
Следствия.
1. Через всякие две точки проходит одна и только одна прямая.
2. Всякие две прямые имеют не более одной общей точки.
3. Через каждые три точки, не принадлежащие одной прямой, проходит одна и только одна плоскость.
4. Через прямую и не лежащую на ней точку проходит одна и только одна плоскость.
5. Через всякие две пересекающиеся прямые проходит одна и только одна плоскость.
Доказываются теоремы о взаимном расположении прямой и плоскости, двух плоскостей.
С помощью аксиом принадлежности нельзя, например, доказать, что множества точек прямых, плоскостей бесконечны.
II группа аксиом — аксиомы порядка.
II 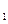 . Если точка
. Если точка  лежит между точкой
лежит между точкой  и точкой
и точкой  , то
, то  ,
,  ,
,  — три различные точки одной прямой и
— три различные точки одной прямой и  лежит также между
лежит также между  и
и  .
.
II 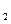 . Если
. Если  и
и  — две точки, то на прямой
— две точки, то на прямой 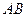 всегда существует по меньшей мере одна точка
всегда существует по меньшей мере одна точка  , что
, что  лежит между
лежит между  и
и  .
.
II 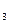 . Из трех точек прямой не более одной точки лежит между двумя другими.
. Из трех точек прямой не более одной точки лежит между двумя другими.
II 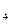 . (Аксиома Паша.) Пусть
. (Аксиома Паша.) Пусть  ,
,  ,
,  — три точки, не лежащие на одной прямой, и
— три точки, не лежащие на одной прямой, и 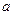 — прямая в плоскости
— прямая в плоскости 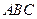 , не проходящая ни через одну из точек
, не проходящая ни через одну из точек  ,
,  ,
,  . Тогда если прямая
. Тогда если прямая 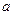 проходит через внутреннюю точку отрезка
проходит через внутреннюю точку отрезка 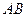 , то она проходит также через внутреннюю точку одного и только одного из двух других отрезков
, то она проходит также через внутреннюю точку одного и только одного из двух других отрезков 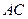 или
или 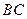 .
.
Из первой и второй групп аксиом можно вывести:
1. Существование бесконечного множества точек на прямой (отрезке).
2. Деление прямой на два луча, плоскости — на две полуплоскости, пространства — на два полупространства.
3. Ряд теорем об угле, ломаной, многоугольнике.
III группа аксиом — аксиомы конгруэнтности.
Конгруэнтность будем обозначать знаком 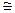 .
.
III 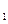 . Если дан отрезок
. Если дан отрезок 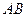 и луч OX, то на луче
и луч OX, то на луче 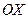 существует такая точка
существует такая точка 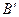 , что
, что 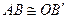 . Всегда
. Всегда 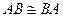 .
.
III 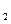 . Если
. Если 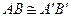 и
и 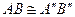 , то
, то 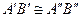 .
.
III 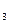 . Пусть
. Пусть 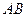 и
и 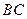 — два отрезка прямой
— два отрезка прямой 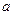 без общих внутренних точек и пусть
без общих внутренних точек и пусть 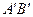 и
и 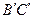 — два отрезка прямой
— два отрезка прямой 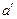 (отличной от
(отличной от 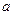 или с ней совпадающей) также без общих внутренних точек. Если
или с ней совпадающей) также без общих внутренних точек. Если 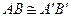 ,
, 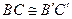 , то
, то 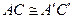 .
.
III 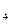 . Пусть дан выпуклый угол
. Пусть дан выпуклый угол 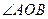 , луч
, луч 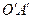 и полуплоскость
и полуплоскость 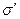 , ограниченная прямой
, ограниченная прямой 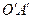 . Тогда в полуплоскости
. Тогда в полуплоскости 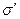 существует один и только один луч
существует один и только один луч 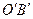 такой, что
такой, что 
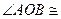

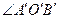 . Всегда
. Всегда 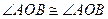 и
и 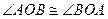 .
.
III 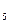 . Если для двух треугольников
. Если для двух треугольников 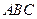 и
и 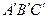 имеем
имеем 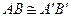 ,
, 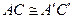 ,
, 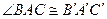 , то
, то 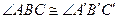 .
.
С помощью групп аксиом I—III можно доказать следующие теоремы:
1. В равнобедренном треугольнике углы при основании конгруэнтны.
2. Первый, второй и третий признаки конгруэнтности треугольников.
3. Существование прямого угла и конгруэнтность прямых углов.
4. Теоремы о делении отрезка и угла пополам.
5. Существование параллельных прямых в плоскости.
6. Свойства внешнего угла треугольника.
Условимся в дальнейшем в ряде случаев вместо термина "конгруэнтный" пользоваться привычным термином "равный". Особенно это относится к углам.
IV группа аксиом — аксиомы непрерывности.
IV 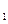 (аксиома Архимеда). Пусть
(аксиома Архимеда). Пусть 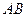 и
и 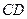 — какие-либо отрезки и пусть на луче
— какие-либо отрезки и пусть на луче 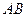 c вершиной
c вершиной  взяты точки
взяты точки  A
A 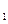 ,
, 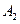 ,
, 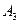 ,..., расположенные так, что
,..., расположенные так, что 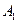 лежит между
лежит между  и
и 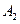 , точка
, точка 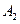 лежит между
лежит между 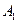 и
и 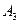 и т. д., причем отрезки
и т. д., причем отрезки 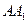 ,
, 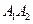 ,
, 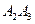 ,... конгруэнтны отрезку
,... конгруэнтны отрезку 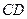 . Тогда существует такой номер
. Тогда существует такой номер 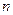 , что точка
, что точка  лежит между
лежит между  и
и 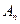 .
.
IV 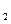 (аксиома Кантора). Пусть на произвольной прямой
(аксиома Кантора). Пусть на произвольной прямой 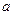 дана бесконечная последовательность отрезков
дана бесконечная последовательность отрезков 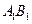 ,
, 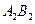 ,
, 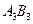 ,..., из которых каждый последующий лежит внутри предыдущего, пусть при этом не существует отрезка, лежащего внутри всех отрезков данной последовательности. Тогда на прямой
,..., из которых каждый последующий лежит внутри предыдущего, пусть при этом не существует отрезка, лежащего внутри всех отрезков данной последовательности. Тогда на прямой 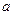 существует одна и только одна точка
существует одна и только одна точка 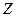 , лежащая внутри всех отрезков
, лежащая внутри всех отрезков 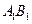 ,
, 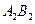 ,
, 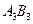 ,...
,...
Вместо аксиом Архимеда и Кантора в эту группу может быть включена только одна аксиома Дедекинда.
IV 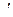 (аксиома Дедекинда). Если все точки отрезка
(аксиома Дедекинда). Если все точки отрезка 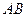 , включая и его концы разбиты на два непустых класса так, что:
, включая и его концы разбиты на два непустых класса так, что:
1) каждая точка отрезка принадлежит одному и только одному из этих классов, точка  принадлежит первому классу, а точка
принадлежит первому классу, а точка  — второму классу;
— второму классу;
2) каждая точка первого класса, отличная от точки  , лежит между
, лежит между  и любой точкой второго класса, то на отрезке
и любой точкой второго класса, то на отрезке 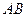 существует одна и только одна такая точка
существует одна и только одна такая точка  , что всякая точка, лежащая между
, что всякая точка, лежащая между  и
и  , принадлежит первому классу, а всякая точка, лежащая между
, принадлежит первому классу, а всякая точка, лежащая между  и
и  , принадлежит второму классу. Сама точка
, принадлежит второму классу. Сама точка  принадлежит либо первому, либо второму классу.
принадлежит либо первому, либо второму классу.
Точка  называется точкой, производящей разбиение, а само разбиение — дедекиндовым разбиением.
называется точкой, производящей разбиение, а само разбиение — дедекиндовым разбиением.
С помощью аксиом I–IV групп можно доказать следующие теоремы:
1. Теорему о пересечении прямой и окружности.
2. Теорему Саккери—Лежандра о сумме углов треугольника.
3. Построить теорию измерения отрезков. 
V группа аксиом — аксиома параллельности.
Через точку, не лежащую на данной прямой в плоскости, ими определяемой, можно провести не более одной прямой, параллельной данной.
Замечание. Из аксиом I—III групп следует, что существуют прямые, лежащие в одной плоскости и не имеющие общих точек, например, два перпендикуляра к одной прямой. Такие прямые называются параллельными. Из факта существования параллельных прямых и из аксиомы параллельности V следует:
через точку, не лежащую на данной прямой, в плоскости, ими определяемой, проходит одна и только одна прямая, параллельная данной.
Как следствие из аксиом I—V верна
Теорема [1.2]. Если сумма углов в любом треугольнике равна двум прямым углам, то имеет место V постулат.
Лекция № _ 5 __.
Тема: ЭЛЕМЕНТЫ ГЕОМЕТРИИ ЛОБАЧЕВСКОГО _
Основные вопросы, рассматриваемые на лекции:
1. Определение плоскости Лобачевского.
2. Свойства параллельных на плоскости Лобачевского.
3. Треугольники и четырехугольники.
4. Угол параллельности. Функция Лобачевского.
 2015-06-24
2015-06-24 7588
7588
