Условимся считать, что все прямые, рассматриваемые нами, являются направленными. Поэтому мы будем обозначать их двумя буквами, например, 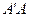 , считая, что точка
, считая, что точка 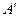 предшествует точке
предшествует точке  . Предполагается также, что точки
. Предполагается также, что точки 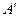 и
и  выбраны так, что рассматриваемые нами точки на этой прямой, лежат между точками
выбраны так, что рассматриваемые нами точки на этой прямой, лежат между точками 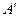 и
и  .
.
Определение [2.1]. Будем говорить, что прямая A’A параллельна прямой В’B в точке P 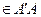 в данном направлении и обозначать A’A
в данном направлении и обозначать A’A 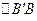 , если:
, если:
1) эти прямые лежат в одной плоскости и не имеют общих точек;
2) для любой точки 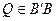 всякий внутренний луч
всякий внутренний луч 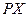 угла
угла 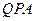 пересекает луч
пересекает луч 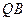 (рис. 17).
(рис. 17).
Теорема [2.1]. Если прямая 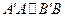 в точке
в точке 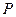 в данном направлении, то
в данном направлении, то 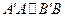 в любой другой точке
в любой другой точке 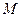 в том же направлении.
в том же направлении.
Теорема [2.2]. (симметричность). Если 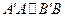 , то
, то 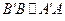 .
.
Теорема [2.3]. (транзитивность). Если 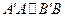 ,
, 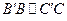 , то
, то 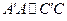 .
.
Замечание. На евклидовой плоскости симметричность и транзитивность параллельности прямых непосредственно следует из определения. В геометрии Лобачевского эти свойства доказываются довольно сложно. Примем их без доказательства.
Теорема [2.4]. Если две прямые при пересечении с третьей образуют равные соответственные углы, или равные накрест лежащие углы, или внутренние односторонние углы, в сумме составляющие 2d, то эти прямые расходятся. 
Следствие 1. Сумма внутренних односторонних углов при двух параллельных, пересекаемых третьей прямой, не равна 2d, она меньше 2d для углов, расположенных от третьей прямой в направлении параллельности. Соответственные углы при параллельных и накрест лежащие углы не равны.
Заметим, что это следствие является прямым отрицанием V постулата.
 2015-06-24
2015-06-24 1962
1962
