Длина отрезка

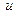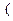Определение [9.1]. Пусть точка B лежит между точками A C A 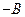–C). Тогда будем говорить, что отрезок AC равен сумме отрезков AB и BC и записывать .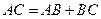

Определение [9.2]. Говорят, что на множестве всех отрезков евклидова пространства 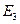задана функция 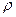длины отрезка, если каждому отрезку 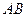поставлено в соответствие некоторое вещественное число 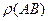так, что:

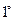
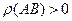для любого отрезка 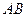(позитивность);

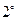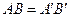если , то 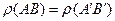(инвариантность);

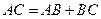если , то 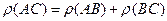(аддитивность);

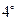существует такой отрезок 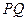, что 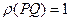(нормированность).

Значение 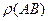функции длины называется длиной отрезка 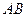, отрезок 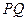— единицей длины или единичным отрезком, свойства 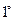— — 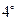аксиомами длины.

Следствие. Если 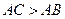, то .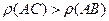

Теорема [9.1]. (существования). Функция длины отрезка, определенная на множестве всех отрезков, существует.

Замечание. Из 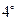следует, что единица измерения 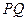зависит от билинейной формы 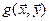, с помощью которой в пространстве 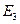определено скалярное произведение. Замена билинейной формы 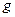приводит к другой единице измерения.

Теорема [9.2]. (единственности). Функция длины отрезка, определенная на множестве всех отрезков, единственна.

О выборе единицы измерения. Справедливо следующее утверждение: любой отрезок может быть принят за единицу измерения.