Треугольники и четырехугольники на плоскости Лобачевского

Теорема [3.1]. Сумма углов в любом треугольнике меньше двух прямых.

Следствие 2. Внешний угол треугольника больше суммы внутренних углов, не смежных с ним.

Следствие 3. Сумма углов любого четырехугольника меньше четырех прямых углов.

Теорема [3.2]. Сумма углов треугольника есть переменная величина.

Определение [3.1]. Дефектом треугольника называется разность 2d и суммы углов треугольника.

Обозначение: 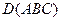— дефект треугольника .

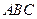Теорема [3.3]. Дефект треугольника 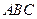обладает следующими свойствами:

1) .

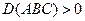2) Если 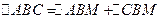, то .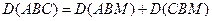

Заметим, что в геометрии Лобачевского справедливы три известных признака равенства треугольников, как следствий из первых трех групп аксиом. Докажем еще один признак равенства треугольников.

Теорема [3.4]. (четвертый признак равенства треугольников). Если три угла одного треугольника равны соответственно трем углам другого треугольника, то эти треугольники равны.

Заметим: из теоремы [19.4] следует, что на плоскости Лобачевского нет подобных треугольников.