Поскольку на плоскости Лобачевского возможны три случая взаимного расположения двух прямых, то на ней существует три различных типа пучков, а именно а) пучок пересекающихся прямых, т. е. множество всех прямых плоскости, проходящих через одну точку — центр пучка; б) пучок расходящихся прямых, т. е. множество всех прямых плоскости, перпендикулярных к некоторой прямой; в) пучок параллельных прямых, т. е. множество всех прямых плоскости, состоящее из некоторой направленной прямой и всех направленных прямых, параллельных ей.
С каждым пучком связаны определенные линии: окружность, эквидистанта, орицикл.
Определение [6.1]. Окружностью называется множество всех точек плоскости, равноудаленных от данной точки (центра окружности).
Это определение относится к абсолютной геометрии, поэтому окружность — линия как евклидовой плоскости, так и плоскости Лобачевского. Все теоремы об окружности, вытекающие из аксиом абсолютной геометрии верны и в той, и в другой геометрии. Отметим те свойства окружности, которые связаны с пучком.
1  . Окружность симметрична относительно любой прямой, проходящей через центр. Такая прямая называется осью окружности.
. Окружность симметрична относительно любой прямой, проходящей через центр. Такая прямая называется осью окружности.
2  . В каждой точке окружности существует касательная, которая перпендикулярна к оси, проходящей через точку касания.
. В каждой точке окружности существует касательная, которая перпендикулярна к оси, проходящей через точку касания.
Таким образом, окружность пересекает свои оси под прямым углом. Поэтому окружность — это ортогональная траектория пучка пересекающихся прямых.
Определение [6.2]. Эквидистантой называется множество всех точек полуплоскости с границей  , равноудаленных от этой прямой — базы эквидистанты. Расстояние от любой точки эквидистанты до базы называется высотой эквидистанты, а прямая, проходящая через точку эквидистанты перпендикулярно к базе, называется осью эквидистанты.
, равноудаленных от этой прямой — базы эквидистанты. Расстояние от любой точки эквидистанты до базы называется высотой эквидистанты, а прямая, проходящая через точку эквидистанты перпендикулярно к базе, называется осью эквидистанты.
Отметим без доказательства некоторые свойства эквидистанты.
1  . Любая прямая, лежащая в плоскости эквидистанты, пересекается с ней не более, чем в двух точках.
. Любая прямая, лежащая в плоскости эквидистанты, пересекается с ней не более, чем в двух точках.
2  . Эквидистанта симметрична относительно любой своей оси.
. Эквидистанта симметрична относительно любой своей оси.
3  . В каждой точке эквидистанты существует касательная, которая перпендикулярна к оси, проходящей через точку касания.
. В каждой точке эквидистанты существует касательная, которая перпендикулярна к оси, проходящей через точку касания.
Таким образом, эквидистанта так же, как и окружность, пересекает свои оси под прямым углом. Поэтому эквидистанта — это ортогональная траектория пучка расходящихся прямых.
Определение [6.3]. Орициклом называется ортогональная траектория пучка параллельных прямых.
Свойства орицикла аналогичны свойствам окружности и эквидистанты. Кроме того, можно показать, что все орициклы равны между собой.
7. Непротиворечивость планиметрии Лобачевского. Независимость V постулата
В этом параграфе будет построена евклидова модель планиметрии Лобачевского, а именно модель Пуанкаре, с целью доказательства содержательной непротиворечивости планиметрии Лобачевского в рамках евклидовой геометрии.
По определению плоскость Лобачевского состоит из элементов двух родов: точек и прямых, связанных тремя основными отношениями "принадлежит", "лежит между", "конгруэнтны", которые удовлетворяют аксиомам I—IV групп аксиоматики Гильберта и аксиоме Лобачевского V 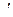 (см. 1).
(см. 1).
На евклидовой плоскости возьмем некоторую прямую 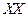 , которая разделит плоскость на две полуплоскости
, которая разделит плоскость на две полуплоскости 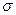 и
и 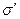 (рис.
(рис.
Определение [7.1]. <<Плоскостью Лобачевского>> (коротко: Л-плоскостью) будем называть открытую евклидову полуплоскость с границей 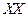 . Прямая
. Прямая 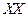 называется абсолютом плоскости Лобачевского.
называется абсолютом плоскости Лобачевского.
Определение [7.2]. <<Точкой Лобачевского>> (короче Л-точкой) будем называть каждую точку открытой полуплоскости 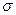 .
.
Замечание. Из определения [23.2] следует, что точки абсолюта не являются точками Лобачевского.
Определение [7.3]. <<Прямой Лобачевского>> (коротко: Л-прямой) будем называть или всякую евклидову полуокружность, лежащую в 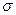 и центр которой принадлежит абсолюту, или всякий открытый луч полуплоскости
и центр которой принадлежит абсолюту, или всякий открытый луч полуплоскости 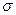 , перпендикулярный абсолюту и начало которого принадлежит абсолюту.
, перпендикулярный абсолюту и начало которого принадлежит абсолюту.
Замечание. Из определения [23.3] следует, что начало луча, задающего Л-прямую, не принадлежит этой Л-прямой, так как не является точкой Лобачевского.
Определение [7.4]. Будем говорить, что <<Л-точка принадлежит Л-прямой>> или она <<лежит>> на этой Л-прямой, если соответствующая евклидова точка принадлежит соответствующей евклидовой прямой или полуокружности.
Определение [7.5]. Пусть  ,
,  ,
,  — три Л-точки, лежащие на Л-прямой
— три Л-точки, лежащие на Л-прямой 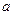 . Будем говорить, что <<Л-точка
. Будем говорить, что <<Л-точка  лежит между Л-точками
лежит между Л-точками  и
и  >>, если евклидова точка
>>, если евклидова точка  лежит между евклидовыми точками
лежит между евклидовыми точками  и
и  на соответствующей полуокружности или луче в евклидовом смысле.
на соответствующей полуокружности или луче в евклидовом смысле.
Определение [7.6]. Два Л-отрезка 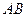 и
и 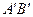 будем называть <<конгруэнтными>>, если существует такая конечная последовательность инверсий с центрами на прямой
будем называть <<конгруэнтными>>, если существует такая конечная последовательность инверсий с центрами на прямой 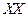 , композиция которых соответствующую дугу или отрезок
, композиция которых соответствующую дугу или отрезок 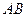 отображает в соответствующую дугу или отрезок
отображает в соответствующую дугу или отрезок 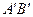 .
.
Теорема [7.1]. Геометрия Лобачевского непротиворечива постольку, поскольку непротиворечива геометрия Евклида.
Согласно критерию независимости (см.?) из этой теоремы следует
Теорема [7.2]. Аксиома V или эквивалентный ей пятый постулат Евклида не зависят от аксиом I—IV абсолютной геометрии.
Лекция № _ 7 __.
Тема: НЕЕВКЛИДОВЫ ГЕОМЕТРИИ
Основные вопросы, рассматриваемые на лекции:
1. Понятие о сферической геометрии.
2. Геометрии Римана и Лобачевского в схеме Вейля.
 2015-06-24
2015-06-24 3483
3483








