Взаимное расположение двух прямых на плоскости Лобачевского

В отличие от евклидовой плоскости на плоскости Лобачевского возможны три случая взаимного расположения двух прямых:

1) прямые пересекаются;

2) прямые параллельны в каком-либо направлении;

3) прямые расходятся в обоих направлениях.

Исследуем расположение одной прямой относительно другой в каждом из этих случаев. Для этого потребуется следующая лемма, относящаяся к абсолютной геометрии.

Лемма [5.1]. Саккери. В четырехугольнике 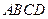с прямыми углами и :

1) ;

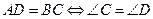2) .

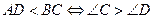Теорема [5.1]. Пусть имеется острый угол 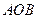. Тогда расстояние от любой точки одной стороны угла до другой стороны неограниченно возрастает по мере удаления точки от вершины угла.

Следствие 5. Пусть 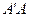и 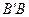— две пересекающиеся в точке 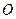прямые. Тогда расстояние от любой точки, лежащей на одной прямой, до другой прямой неограниченно возрастает по мере удаления этой точки от 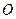в обе стороны.

Теорема [5.2]. Пусть 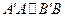. Тогда расстояние от любой точки одной прямой до другой прямой неограниченно уменьшается при перемещении этой точки в направлении параллельности и неограниченно возрастает в противоположном направлении.

Теорема [5.3]. Две расходящиеся прямые не могут иметь более одного общего перпендикуляра.

Теорема [5.4]. Две расходящиеся прямые имеют общий перпендикуляр.

Следствие 6. Две расходящиеся прямые имеют один и только один общий перпендикуляр.

Теорема [5.5]. Пусть 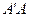и 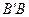— две расходящиеся прямые и 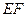— их общий перпендикуляр (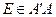, 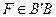). Тогда расстояние от любой точки, лежащей на одной прямой, до другой прямой неограниченно возрастает по мере удаления этой точки в обоих направлениях от точки пересечения этой прямой с общим перпендикуляром.