Эллиптическая геометрия Римана.
Определение [2.1]. Пусть 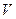 — трехмерное векторное евклидово пространство и
— трехмерное векторное евклидово пространство и 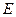 —некоторое непустое множество, элементы которого назовем точками. Множество
—некоторое непустое множество, элементы которого назовем точками. Множество 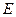 называется эллиптической плоскостью Римана, если задано отображение
называется эллиптической плоскостью Римана, если задано отображение 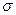 пространства
пространства 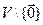 на множество
на множество 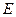 , причем:
, причем:
1) 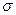 — сюръекция, т. е. каждая точка из
— сюръекция, т. е. каждая точка из 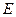 является соответственной для какого-то ненулевого вектора;
является соответственной для какого-то ненулевого вектора;
2) две точки из 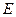 совпадают тогда и только тогда, когда задающие их векторы коллинеарны.
совпадают тогда и только тогда, когда задающие их векторы коллинеарны.
Построим эллиптическую плоскость с помощью сферы.
В качестве векторного пространства 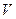 возьмем множество 3.5cm всех векторов евклидова пространства
возьмем множество 3.5cm всех векторов евклидова пространства 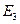 . Каждый такой ненулевой вектор
. Каждый такой ненулевой вектор 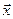 можно задать направленным отрезком, отложенным от точки
можно задать направленным отрезком, отложенным от точки 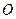 — центра некоторой сферы с радиусом
— центра некоторой сферы с радиусом 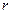 . Через центр
. Через центр 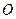 проведем в направлении вектора
проведем в направлении вектора 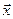 прямую
прямую  , которая пересечет сферу в двух диаметрально противоположных точках
, которая пересечет сферу в двух диаметрально противоположных точках  и
и 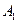 . Обозначим через
. Обозначим через 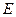 множество всех пар диаметрально противоположных точек сферы. Таким образом, каждому вектору
множество всех пар диаметрально противоположных точек сферы. Таким образом, каждому вектору 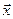 поставлена в соответствие единственная точка множества
поставлена в соответствие единственная точка множества 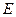 — пара диаметрально противоположных точек
— пара диаметрально противоположных точек  и
и 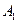 сферы. Это соответствие, как нетрудно установить, обладает свойствами 1 и 2, указанными в определении эллиптической плоскости. Следовательно, построенное множество
сферы. Это соответствие, как нетрудно установить, обладает свойствами 1 и 2, указанными в определении эллиптической плоскости. Следовательно, построенное множество 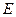 является эллиптической плоскостью Римана. Иначе говоря, эллиптическая плоскость Римана — это сфера с отождествленными диаметрально противоположными точками. Роль прямых на эллиптической плоскости играют большие окружности с отождествленными диаметрально противоположными точками. Отметим два интересных факта:
является эллиптической плоскостью Римана. Иначе говоря, эллиптическая плоскость Римана — это сфера с отождествленными диаметрально противоположными точками. Роль прямых на эллиптической плоскости играют большие окружности с отождествленными диаметрально противоположными точками. Отметим два интересных факта:
1) на эллиптической плоскости Римана всякие две прямые пересекаются;
2) в эллиптической геометрии Римана сумма углов треугольника больше 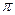 (см. следствие 2).
(см. следствие 2).
Гиперболическая геометрия Лобачевского.
Гиперболическая плоскость получается аналогично, но для этого надо заменить евклидово пространство 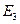 псевдоевклидовым пространством
псевдоевклидовым пространством 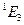 . В свою очередь пространство
. В свою очередь пространство 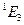 определяется с помощью системы аксиом Вейля, в которой аксиома 4 (см. определение? евклидова пространства) о скалярном квадрате вектора (
определяется с помощью системы аксиом Вейля, в которой аксиома 4 (см. определение? евклидова пространства) о скалярном квадрате вектора (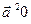 и
и 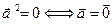 ) заменена следующей аксиомой:
) заменена следующей аксиомой:
4’ Существует ортонормированный базис { 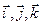 } такой, что
} такой, что 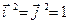 ,
, 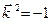 .
.
В пространстве 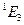 длина вектора
длина вектора 
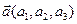 находится по формуле
находится по формуле 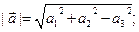 расстояние между точками A(x
расстояние между точками A(x 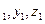 ) и B(x
) и B(x 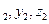 ) равно
) равно 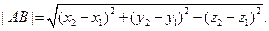

Значит, квадраты длин векторов и расстояний между точками могут выражаться положительным, отрицательным или равным нулю числом.
В псевдоевклидовом пространстве на сферах роль прямых, так же как на сферах в евклидовом пространстве, играют сечения сфер плоскостями, проходящими через центр, которые также будем называть большими окружностями. Под расстоянием между двумя точками будем понимать (псевдоевклидову) длину соединяющей их дуги большой окружности.
Рассмотрим в пространстве 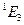 сферу мнимого радиуса с уравнением
сферу мнимого радиуса с уравнением 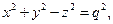 где радиус
где радиус 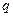 является мнимым числом, т. е.
является мнимым числом, т. е. 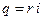 (
(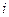 — мнимая единица). Запишем уравнение этой сферы в виде
— мнимая единица). Запишем уравнение этой сферы в виде
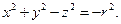 (2.6)
(2.6)
Заметим, что в евклидовом пространстве уравнение (1) есть уравнение двуполостного гиперболоида.
Определение [2.2]. Назовем гиперболической плоскостью сферу мнимого радиуса в псевдоевклидовом пространстве с отождествленными диаметрально противоположными точками.
Гиперболическую плоскость можно представлять себе как одну полость двуполостного гиперболоида в евклидовом пространстве. Роль прямой играет ветвь гиперболы, при этом плоскость, в которой эта гипербола лежит, проходит через центр гиперболоида.
Пусть 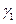 и
и 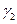 —две гиперболы,
—две гиперболы, 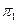 и
и 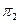 — плоскости, в которых они лежат, и пусть эти плоскости пересекаются по прямой
— плоскости, в которых они лежат, и пусть эти плоскости пересекаются по прямой  . Тогда:
. Тогда:
1) если  проходит внутри гиперболоида, то
проходит внутри гиперболоида, то 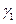 и
и 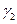 пересекаются;
пересекаются;
2) если  проходит вне гиперболоида, то
проходит вне гиперболоида, то 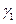 и
и 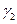 не пересекаются;
не пересекаются;
1) если  является образующей асимптотического конуса гиперболоида, то
является образующей асимптотического конуса гиперболоида, то 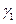 и
и  снова не пересекаются; в этом случае они называются параллельными.
снова не пересекаются; в этом случае они называются параллельными.
Это позволяет сделать вывод, что геометрия сферы мнимого радиуса в трехмерном псевдоевклидовом пространстве есть геометрия Лобачевского. Поэтому геометрию Лобачевского называют также гиперболической геометрией Лобачевского.
Учебные наглядные пособия и ЦОР, используемые на лекциях
(при необходимости)
- Электронное пособие «Основания геометрии» (Презентация)
 2015-06-24
2015-06-24 767
767








