И семинарским занятиям

1. ВВЕДЕНИЕ: Учебные и воспитательные цели.

- Применение теоретических положений к решению конкретных задач оснований геометрии.

- Развитие математической культуры.

2. ИСПОЛЬЗУЕМАЯ ЛИТЕРАТУРА

1. Атанасян Л.С.и др. Сборник задач по геометрии.- Часть 2.- М.: Просвещение, 1975.

2. Атанасян Л.С., Базылев В.Т. Геометрия. Ч.2. - М.: Просвещение, 1987.

3. Львова Л.В. Геометрия. Основания геометрии: учебное пособие. – Барнаул: Изд-во БГПУ, 2005. 104 с.

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № _ 1 _

Тема: Общие вопросы аксиоматики. _

Продолжительность _2 _ часа

План практического или семинарского занятия:

1. Вопросы, выносимые на обсуждение

Понятие о математической структуре. Непротиворечивость, независимость и полнота системы аксиом.

2. Краткие теоретические материалы

Рекомендуется изучить §§ 1.2 – 1.4 в учебном пособии [3].

3. Практические задачи, задания, упражнения.

Для сокращения записей матрицу с элементами 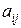( 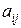– действительные числа), имеющую р строк и q столбцов, будем обозначать через. 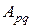. Например, А₁₃ = (a ₁₁ а ₁₂ а ₁₃ ),

, , .

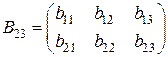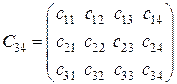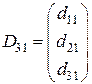Сумму матриц A_pq и B_pq будем обозначать через A_pq + B_pq,для произведения матриц примем обычные обозначения, например: A_pq • B_qr = C_pr. Матрица, транспонированная матрице A_pq,обозначается через A_qp.

1. Назовем вектором любую квадратную матрицу А_рр (р – фиксированное натуральное число); суммой векторов А_рр и В_рр – матрицу А_рр + В_рp, а произведением числа λна вектор А_рр – матрицу λ А_рр. Показать, что при этом все аксиомы векторного пространства V₃, кроме III₂, выполняются.

2. Дополним соглашения, сформулированные в задаче 1: скалярным произведением векторов А_рр и В_рр назовем число

.

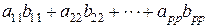Проверить выполнимость аксиом скалярного произведения V₁ – V₄.

3. Назовем вектором любую матрицу А_зъ точкой — любую матрицу М₁₃, суммой векторов А₃₁ и В₃₁ — вектор А₃₁ + В₃₁ произведением вектора А₃₁ на число λ— вектор А₃₁. Скалярным произведением векторов А₃₁ и В₃₁ назовем число:

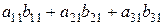
4. Паре точек 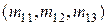и 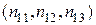ставится в соответствие вектор

,

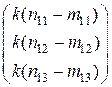где 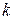– фиксированное число, отличное от нуля. Показать, что при этом выполняются все аксиомы I – V групп системы аксиом Вейля.

5. Пользуясь задачей 3, доказать, что система аксиом Вейля непротиворечива.

6. Показать, что в системе аксиом Вейлякаждая из аксиом III₁ и III₂ не зависит от остальных аксиом.

7. Показать, что в системе аксиом ∑_W аксиома V₄ не зависит от остальных аксиом.

8. Показать, что в системе аксиом ∑_W аксиома IV₁ не зависит от остальных аксиом.

4. Вопросы и задания студентам для самостоятельной работы.

1. Сохраним все соглашения задачи 1, за исключением одного: суммой векторов А_рр и В_рр назовем вектор А_рр • В_рр. Проверить выполнимость аксиом I₁ – I₄, II₁ – II₄.

2. Будут ли выполнены все аксиомы Вейля евклидова пространства 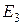, если в условиях задачи 3 соответствие между парой точек и вектором ввести следующим образом: паре точек 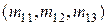и 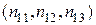ставится в соответствие вектор

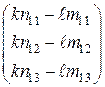
где k и ℓ — фиксированные различные действительные числа, причем kℓ ≠ 0?

3. Доказать, что в системе аксиом ∑_W аксиома IV₂ не зависит от остальных аксиом.

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № __ 2 ____

Тема: Система аксиом Вейля евклидова пространства______

Продолжительность _2 _ часа

1. Вопросы, выносимые на обсуждение

Непротиворечивость и полнота системы аксиом Вейля. Независимость аксиом.Определение простейших фигур.

2. Краткие теоретические материалы

Рекомендуется изучить § 1.7 в учебном пособии [3].

Практические задачи, задания, упражнения.

1. Показать, что в любом треугольнике ABC имеет место соотношение:

|АС|<|АВ| + |ВС|.

2. Показать, что в любом треугольнике ABC имеет место соотношение:

| ВС\ = | ВА | cos B + | С А | cos С.

3. Доказать, что у равнобедренного треугольника углы при основании равны. Сформулировать и доказать обратное предложение.

4. Доказать, что все точки биссектрисы угла равноудалены от сторон угла. Пользуясь этим, показать, что биссектрисы треугольника пересекаются в одной точке.

5. Если а и b — две различные параллельные прямые, а α и β – две пересекающиеся плоскости, удовлетворяющие условию: а 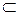α, b 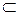β, то плоскости α и β пересекаются по прямой, параллельной прямым а и b. Доказать.

6. По аналогии с понятием угла ввести понятие двугранного угла и понятия внутренней и внешней областей угла.

7. Доказать, что если один конец отрезка принадлежит внутренней области, а другой конец – внешней, то отрезок пересекает грани или ребро этого угла.

8. Доказать теорему о трех перпендикулярах: пусть ℓ — прямая, не перпендикулярная плоскости α, а 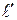—проекция этой прямой на плоскость. Если 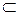m α и m 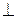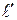, то т 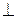ℓ. Обратно: если 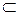m α и m 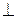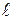, то т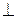

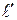
9. Пусть а и b — скрещивающиеся прямые. Доказать: 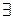!α (α 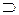a, α || b).

10. Пусть а и b — скрещивающиеся прямые. Доказать, что существует одна и только одна прямая, которая пересекает данные прямые и ортогональна им обеим.

4. Вопросы и задания студентам для самостоятельной работы.

1. Показать, что в любом треугольнике ABC имеет место соотношение:

| ВС| ²= | AС |² + | АВ |² – 2 | АВ| |AС | cos A.

2. Показать, что в любом треугольнике ABC имеет место соотношение:

| ВС\ = | ВА | cos B + | С А | cos С.

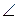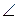3. Доказать, что если в треугольнике ABC имеем: | АВ|>|АС|, то С > В.

4. Доказать, что прямые, содержащие высоты любого треуголь­ника, пересекаются в одной точке.

5. Доказать, что медианы треугольника пересекаются в одной точке.

6. Если две параллельные плоскости пересекаются третьей плоскостью, то линии пересечения параллельны. Доказать.

7. Доказать теорему: плоскость α единственным образом разбивает все точки пространства, не принадлежащие плоскости, на два множества так, что если точки А и В принадлежат одному множеству, то отрезок АВ не пересекает плоскость, а если разным множествам, то этот отрезок пересекает плоскость. Пользуясь этим предложением, ввести понятие полупространства.

8. Две плоскости, параллельные между собой и не параллельные ребру двугранного угла, пересекают его по двум конгруэнтным углам. Доказать.

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № ___ 3 ____

Тема: Длина отрезка. Площадь многоугольника. Равновеликость и равносоставленность._____

Продолжительность _2 _ часа

План практического или семинарского занятия:

1. Вопросы, выносимые на обсуждение

Площадь треугольника, параллелограмма, трапеции. Теорема Бойяи – Гервина.

2. Краткие теоретические материалы

Рекомендуется изучить [3], §§ 9 – 10.

3. Практические задачи, задания, упражнения.

1. В правильной четырехугольной пирамиде SABCD площадь сечения, проведенного через диагональ AC основания параллельно ребру SB равна S ₀. Построить сечение пирамиды плоскостью, проходящей через середины двух смежных сторон основания и середину высоты пирамиды, и найти площадь этого сечения.

2. Дан куб ABCDA ₁ B ₁ C ₁ D ₁. Плоскость сечения проходит через вершину A ₁, середину ребра В ₁ С ₁ и центр грани DCC ₁ D ₁, рассекая куб на две части. Найти отношение объемов этих частей.

3. В правильной четырехугольной призме проведены два параллельных сечения: первое проходит через середины двух смежных сторон основания и через середину отрезка ОО ₁, соединяющего центры оснований, второе делит отрезок ОО ₁ в отношении 1:3. Зная, что площадь первого сечения равна 5, найти площадь второго.

4. В основании треугольной пирамиды SABC лежит прямоугольный треугольник ABC с прямым углом АСВ, ребро SA перпендикулярно плоскости основания. В пирамиду вписан шар, радиус которого равен 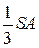. Через вершину S и точку касания шара с плоскостью основания пирамиды проведена плоскость, параллельная ребру ВС. Эта плоскость делит поверхность шара на части, площади которых относятся как 1:4. Найти величину угла ВАС.

1. Вопросы и задания студентам для самостоятельной работы.

1. В правильной четырехугольной пирамиде SABCD с боковым ребром SA = b и стороной основания АВ = а проведена плоскость через середины ребер АВ, ВС и SD.

а) Построить сечение пирамиды указанной плоскостью.

б) Найти площадь сечения.

в) Доказать, что плоскость сечения рассекает пирамиду на два равновеликих многогранника.

2. В прямоугольном параллелепипеде ABCDA ₁ B ₁ C ₁ D ₁ длины ребер АВ=а, AD = b, АА ₁ = с; О ₁ —центр основания A ₁ B ₁ C ₁ D ₁; О —центр основания АВСD; S — точка, делящая отрезок ОО ₁ в отношении 1:3.

Плоскость сечения проходит через точку S параллельно диагонали СА ₁ параллелепипеда и диагонали B ₁ D ₁ его основания. Построить сечение и найти его площадь.

3. Ребро куба равно а. Построить сечение куба плоскостью, проходящей через центр куба перпендикулярно его диагонали, и вычислить площадь сечения.

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № __ 4 _____

Тема: Система аксиом Гильберта _

Продолжительность _2 _ часа

План практического или семинарского занятия:

1. Вопросы, выносимые на обсуждение

Следствия всех групп аксиом Гильберта.

2. Краткие теоретические материалы

Рекомендуется изучить [3], § 14.

3. Практические задачи, задания, упражнения.

1. Убедиться в том, что в интерпретации, описанной ниже, выполняются все аксиомы I, II и IV групп системы аксиом Гильберта евклидовой плоскости .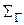

Точкой называется пара действительных чисел (х, у), взятых в определенном порядке.

Прямой называется всякое уравнение вида kx – у + b = 0 или – х + b = 0, где k и b – произвольные действительные числа.

Пусть различные точки 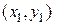, , 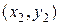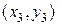принадлежат одной прямой; точка 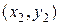называется лежащей между 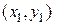и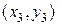

если при x ₂ – x ₃ 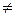0 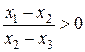, а при х₂ = х ₃: .

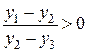2. Показать, что в системе аксиом Гильберта каждое из следующих предложений эквивалентно аксиоме параллельности:

а) сумма внутренних углов треугольника равна двум прямым;

б) если различные прямые а и b не перпендикулярны, то перпендикуляр, проведенный в любой точке прямой а, пересекает прямую b;

в) существует четырехугольник с четырьмя прямыми углами;

г) существуют три различные коллинеарные точки, равноудаленные отданной прямой;

д) угол, под которым виден диаметр окружности из какой-либо точки этой окружности, конгруэнтен прямому углу;

е) перпендикуляры, проведенные к серединам сторон любого треугольника, пересекаются в одной точке.

3. Пользуясь только аксиомами I группы Гильберта, доказать,, что каждой плоскости принадлежат по крайней мере три точки, не лежащие на одной прямой.

4.Доказать, что в системе аксиом Гильберта 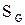аксиома III₅ не зависит от остальных аксиом.

5. Пусть Ј — некоторая интерпретация системы аксиом Гильберта. Построить новую интерпретацию J ´ следующим образом.

В интерпретации Ј ' все основные понятия, встречающиеся в аксиомах, определяются так же, как и в интерпретации Ј, за исключением конгруэнтности отрезков. В Ј ' любые два отрезка считаются конгруэнтными. Будет ли Ј ' интерпретацией системы аксиом ?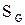

6. Выпуклый четырехугольник ABCD, у которого углы А и В прямые и AD 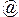BC, называется четырехугольником Хайяма—Саккери, АВ – нижнее основание, CD – верхнее основание. Пользуясь аксиомами I—IV групп, доказать, что внутренние углы при верхнем основании четырехугольника Хайяма—Саккери конгруэнтны и что эти углы не могут быть тупыми.

4. Вопросы и задания студентам для самостоятельной работы.

1. Точкой называется каждая из следующих троек чисел: (0, 0, 0), (1, 0, 0), (0, 1, 0), (0, 0, 1). Числа, определяющие точку, назовем ее координатами.

Прямой назовем каждую из следующих систем уравнений:

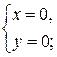
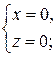
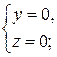
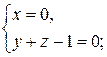
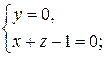
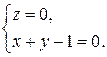
Плоскостями назовем следующие четыре уравнения:

х = 0, y = 0, z = 0, x + y + z— 1=0.

Точка принадлежит прямой тогда и только тогда, когда ее координаты удовлетворяют уравнениям, определяющим прямую. Аналогично определяется принадлежность точки и плоскости.

Показать, что в построенной интерпретации выполняются все аксиомы группы I системы аксиом Гильберта.

2. Показать, что в системе аксиом Гильберта каждое из следующих предложений эквивалентно аксиоме параллельности:

а) существуют три различные коллинеарные точки* равноудаленные отданной прямой;

б) существуют два подобных, но не конгруэнтных треугольника;

в) через любые три точки, не лежащие на одной прямой, проходит окружность;

3. Пользуясь только аксиомами I и II групп, доказать, что множество внутренних точек отрезка не пусто.

4. Пусть а и b —две непересекающиеся прямые на плоскости. Предложение: множество {ρ(M, a)| M b) ограничено – эквивалентно V постулату. Доказать.

5. Предложение: через любую внутреннюю точку угла, меньшего развернутого, можно провести прямую, пересекающую обе стороны угла, – эквивалентно V постулату». Доказать.

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № ___ 5 ___

Тема: Контрольная работа №1 _

Продолжительность _2 _ часа

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № __ 6 ___

Тема: Элементы геометрия Лобачевского _______

Продолжительность _2 _ часа

План практического или семинарского занятия:

1. Вопросы, выносимые на обсуждение

Функция Лобачевского. Взаимное расположение прямых. Окружность, эквидистанта, орицикл. Модель Кэлли – Клейна плоскости Лобачевского.

2. Краткие теоретические материалы

Рекомендуется изучить [3], § 2.3.

3. Практические задачи, задания, упражнения.