Предполагается, что задачи, помещенные в этом параграфе, решаются на основе аксиом I –IV групп системы аксиом Гильберта и аксиомы параллельности V´ Лобачевского. Параллельные прямые предполагаются направленными.
1. Пусть 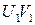 ||
|| 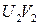 . Доказать, что если прямая UV лежит между
. Доказать, что если прямая UV лежит между 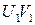 и
и 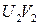 и не пересекает ни одну из них, то она параллельна данным прямым.
и не пересекает ни одну из них, то она параллельна данным прямым.
2. Пусть 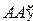 и
и 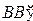 — две различные прямые. Прямая АВ называется прямой равного наклона этих прямых, если
— две различные прямые. Прямая АВ называется прямой равного наклона этих прямых, если 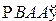
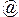
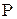 ABB', точки А' и В' лежат по одну и ту же сторону от прямой АВ. Доказать предложения:
ABB', точки А' и В' лежат по одну и ту же сторону от прямой АВ. Доказать предложения:
а) любые две прямые равного наклона на непересекающихся прямых
АА' и ВВ' отсекают конгруэнтные отрезки;
б) через каждую точку одной из двух данных непересекающихся
прямых АА' и ВВ' проходит одна и только одна прямая равного наклона.
Справедливы ли эти предложения, если прямые АА' и ВВ' пересекаются?
3. Пусть в четырехугольнике ABCD углы А и D прямые. Доказать предложения:
а) если [ CD ] 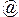 [ АВ ], то
[ АВ ], то 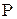 В
В 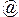
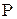 С;
С;
б) если | CD| > | АВ |, то 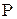 B >
B > 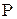 С.
С.
4. Пусть ABCD — четырехугольник Саккери с прямыми углами А и D и боковыми сторонами АВ и CD ([ АВ ] 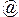 [CD]). Доказать следующие предложения:
[CD]). Доказать следующие предложения:
а) 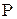 В
В 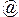
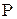 С < d, где d — прямой угол;
С < d, где d — прямой угол;
б) прямая, соединяющая середины оснований AD и BС, перпендикулярна этим основаниям.
5. На сторонах угла BOA взяты точки В' и А' так, что В лежит между О и В', а A лежит между О и A'. Доказать, что дефект треугольника ОАВ меньше дефекта треугольника ОА'В'.
6. Доказать теорему: если серединные перпендикуляры двух сторон треугольника расходятся, то серединный перпендикуляр третьей стороны расходится с каждым из них и существует прямая, которая перпендикулярна всем трем серединным перпендикулярам.
7. Доказать, что угол, под которым виден диаметр [АВ] окружности из любой точки этой окружности, не совпадающей с концами диаметра, меньше прямого угла.
8. Доказать, что существует «треугольник с нулевыми углами», т. е. существуют три прямые AА', ВВ' и 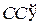 , удовлетворяющие условиям: AА' || С'С, А'А || ВВ', В'В ||
, удовлетворяющие условиям: AА' || С'С, А'А || ВВ', В'В || 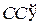 .
.
9. Доказать, что любые два треугольника с нулевыми углами (см. предыдущую задачу) конгруэнтны.
 2015-06-24
2015-06-24 901
901








