Вопросы и задания для самостоятельной работы студентов

Специальность 050201.65 математика с доп. специальностью

код наименование

КОНТРОЛЬНЫЕ ВОПРОСЫ и ЗАДАНИЯ

1. Систему аксиом Вейля аффинного пространства можно сформулировать состоящей из двух аксиом 1–2 [1]. Доказать, что первая аксиома не зависит от второй.

2. Доказать, что вторая аксиома системы аксиом Вейля не зависит от первой аксиомы.

3. Предложение: существуют подобные, но неконгруэнтные треугольники, эквивалентно V постулату. Доказать.

4. Предложение: около всякого треугольника можно описать окружность, эквивалентно V постулату. Доказать.

5. Пусть 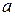и 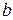– непересекающиеся прямые на плоскости. Предложение: множество 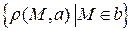, эквивалентно V постулату. Доказать.

6. Предложение: через любую внутреннюю точку угла, меньшего развернутого, можно провести прямую, пересекающую обе стороны угла, эквивалентно V постулату. Доказать.

7. Пользуясь только аксиомами I группы Гильберта, доказать, что каждой плоскости принадлежат по крайней мере три точки, не лежащие на одной прямой.

8. Пользуясь только аксиомами I и II групп Гильберта, доказать, что множество внутренних точек отрезка не пусто.

9. Выпуклый четырехугольник 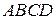, у которого углы 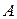и 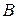прямые и 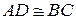, называется четырехугольником Саккери, 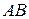– нижнее основание, 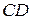– верхнее основание. Пользуясь аксиомами абсолютной геометрии, доказать, что внутренние углы при верхнем основании четырехугольника Саккери конгруэнтны. Доказать также, что эти углы не могут быть тупыми.

10. Доказать, что каждая из аксиом Вейля 1–2 независима от другой.

11. Построить интерпретацию I группы аксиом школьного курса геометрии на конечном множестве.

12. Пользуясь аксиомами школьного курса геометрии, доказать, что:

1) каждый отрезок содержит бесконечное множество точек;

2) каждая плоскость содержит бесконечное множество точек, не лежащих на одной прямой;

3) пространство содержит бесконечное множество точек, не лежащих на одной плоскости.

13. Пользуясь аксиомами школьного курса геометрии, доказать, что:

1) сумма величин внутренних углов любого треугольника равна π:

2) существуют подобные, но неконгруэнтные треугольники;

3) около всякого треугольника можно описать окружность;

4) через любую внутреннюю точку угла, меньшего развернутого, можно провести прямую, пересекающую обе стороны угла.

15. Доказать, что из аксиом Вейля аффинного пространства следует аксиома параллельности.

16. Используя скалярное произведение векторов, доказать теоремы о плоских углах трехгранного угла: сумма любых двух плоских углов трехгранного угла больше третьего плоского угла, а сумма всех трех плоских углов меньше 360º.

17. Даны три точки, не принадлежащие одной прямой. Используя аксиомы принадлежности, расстояния и порядка, доказать, что через эти точки нельзя провести двух различных окружностей.

18. Используя аксиомы принадлежности, расстояния и порядка, доказать, что в данной полуплоскости с границей 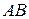не существует двух различных точек 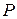и 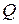таких, что , .

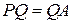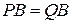19. Доказать, что на эллиптической плоскости 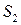симметрия относительно прямой 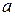и центральная симметрия относительно точки 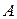совпадают, если точка 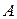является полюсом прямой .

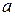20. Доказать, что на эллиптической плоскости существуют только три типа движений: поворот на угол, отличный от π, центральная (или осевая) симметрия и тождественное преобразование.

21. Найти зависимость между сторонами четырехугольника, чтобы около него можно было описать окружность.

22. Доказать, что на плоскости Лобачевского вписанный в окружность угол, опирающийся на диаметр, острый.

23. Доказать, что длина отрезка, соединяющего середины двух сторон треугольника, больше половины длины третьей стороны.

24. Доказать, что на плоскости Лобачевского вписанный в окружность угол, опирающийся на диаметр, острый.

25. Доказать, что длина отрезка, соединяющего середины двух сторон треугольника, больше половины длины третьей стороны.

26. Доказать, что если серединные перпендикуляры двух сторон треугольника параллельны, то серединный перпендикуляр третьей стороны параллелен первым двум в одном и том же направлении

27. Доказать, что сторона правильного шестиугольника боль­ше радиуса окружности, описанной около шестиугольника,

28. Доказать, что если углы одного треугольника конгруэнт­ны углам другого треугольника, то треугольники конгруэнтны.

29. На модели Кэли — Клейна плоскости Лобачевского по­строить середину данного отрезка, биссектрису данного угла.

30. На модели Кэли — Клейна на данном луче отложить от его начала отрезок, конгруэнтный данному.

31. На модели Кэли — Клейна для данного острого угла по­строить соответствующий ему отрезок параллельности и обратно; для данного отрезка построить соответствующий ему угол парал­лельности.

32. Возьмем на плоскости Лобачевского какой-либо угол А'АА”, меньший развернутого. Доказать, что существует прямая и притом единственная, параллельная в одном своем направлении прямой АА’ а в другом направлении — прямой АА".

33. Для любых двух различных параллельных прямых АА', (ВВ) существует прямая и единственная, которая в одном своем направлении параллельна прямой АА', а в другом — прямой ВВ'. Доказать.

34. Доказать предложения:

35. а) если АА' || ВВ' и АВ — прямая равного наклона этих прямых, то перпендикуляр, восставленный в середине отрезка АВ,, параллелен прямым АА' и ВВ';

36. б) множество середин всех отрезков равного наклона двух параллельных прямых принадлежит прямой, параллельной данным прямым.

37. Пусть АА', ВВ' и 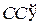— различные попарно параллель­ные прямые. Доказать, что если АВ — прямая равного наклона прямых АА' и ВВ', а ВС — прямая равного наклона прямых ВВ' и 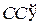, то АС — прямая равного наклона для прямых АА' и .

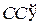38. Сформулировать и доказать предложения, обратные предложе­ниям а) и б) задачи 5.

39. Пусть ABCD — четырехугольник Саккери с прямыми углами А и D и боковыми сторонами АВ и CD ([ АВ ] 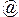[CD]). Доказать следующие предложения:

40. в) основания AD и ВС принадлежат расходящимся прямым;

41. г) основание AD меньше основания ВС.

42. Доказать теорему: если серединные перпендикуляры двух сторон треугольника параллельны, то серединный перпендикуляр третьей стороны параллелен им обоим.

43. Доказать, что на плоскости Лобачевского существуют тре­угольники, удовлетворяющие условиям: серединные перпендикуляры сторон принадлежат пучку: а) пересекающихся прямых; б) парал­лельных прямых; в) расходящихся прямых.

44. На евклидовой плоскости дана окружность (абсолют), внутренние точки которой вместе с точками окружности обозначим через Q. Л-точки, Л-прямые и принадлежность Л-точек и «/7-прямых определяются так же, как и в задаче 3. Взаимно-однозначное преобразование точек множества Q называется Л-движением, если оно точки абсолюта переводит в точки абсолюта, любую хорду абсолюта пере­водит в хорду абсолюта и сохраняет сложное отношение четырех то­чек. Фигура F называется конгруэнтной фигуре F', если существует такое Л-движение, которое фигуру F переводит.в фигуру 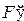. Показать, что в построенной интерпретации выполняются все аксиомы I, II и III групп системы аксиом Гильберта и аксиома параллельности 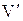Лобачевского.

45. Дан угол, построить отрезок так, чтобы данный угол был углом параллельности, соответствующим этому отрезку.

46. Дан отрезок АВ и луч k', исходящий из точки А'. На луче k' найти такую точку В', чтобы отрезок АВ был конгруэнтен отрезку А'В'.

47. Дан угол (h, k). Построить луч 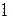так, чтобы луч k был бис­сектрисой угла (h, ).

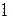48. Даны две расходящиеся прямые U₁V₁ и U₂V₂. Построить общий перпендикуляр данных прямых.

49. Доказать, что во всяком сферическом треугольнике сумма двух углов без третьего меньше π, а сумма трех его углов принадле­жит интервалу (π, 3π).

50. В сферическом треугольнике против конгруэнтных углов лежат конгруэнтные стороны. Доказать.

51. Доказать, что в сферическом треугольнике против боль­шего угла лежит и большая сторона.

52. В сферическом треугольнике против большей стороны ле­жит и больший угол. Доказать.

53. Доказать, что композиция двух центральных симметрии есть поворот. Построить центр поворота и найти величину угла поворота.

54. Доказать, что на эллиптической плоскости существуют только три типа перемещений: поворот на угол, отличный от π, центральная (или осевая) симметрия и тождественное преобразо­вание.

55. Доказать, что угол между двумя прямыми равен расстоя­нию между их полюсами или расстоянию между точками пересече­ния этих прямых с их общим перпендикуляром (принимая г = 1).

56. Доказать, что три точки, не принадлежащие одной прямой, являются вершинами четырех треугольников и для каждого из них выполняется неравенство треугольника.

57. Доказать, что на плоскости Лобачевского вписанный в окружность угол, опирающийся на диаметр, острый.

58. Через данную точку, не принадлежащую орициклу, про­вести касательную к орициклу.

59. Доказать, что композиция двух центральных симметрии есть сдвиг. Чему равно расстояние сдвига?

60. Построить орицикл, проходящий через данную точку и касающийся данной прямой.