Характеристические функции

Доказательство тождеств методом 2-х включений часто бывает весьма громоздким, и при построении доказательств ход рассуждений не всегда очевиден. Одним из методов, не требующих угадывания способа доказательств, является метод характеристических функций.

Характеристическая функция (ХФ) χ_А множества А 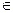U есть функция, отображающая универсальное множество U в двухэлементное множество {0,1}: χ_А(х) = .

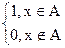Из определения ХФ множества А вытекает справедливость тождества: (χ_А(х))² = 1.

Выразим ХФ пересечения множеств А∩В через ХФ этих множеств. Из определения ХФ следует, что она должна принимать значение 1 для тех элементов, которые принадлежат множествам А и В одновременно, и значение 0 в противном случае. Легко видеть, что функция χ_А∩В = χ_А · χ_В удовлетворяет этому требованию.

Далее, если мы посмотрим на функцию χ_А + χ_В, то увидим, что она принимает значение 1 на каждом из множеств А и В и значение 2 на пересечении множеств. Поэтому, чтобы получить ХФ объединения множеств, нужно ввести поправку к сумме ХФ: χ_АUВ = χ_А + χ_В – χ_А · χ_В

По определению дополнения χ_Ā = 1– χ_А. Действуя аналогичным образом, получаем:

ХФ разности имеет вид χ_А\B = χ_А – χ_А χ_А;

а симметрической разности: χ_АóВ = χ_А + χ_В – 2χ_А · χ_В = (χ_А – χ_В)².

Метод доказательства тождеств теории множеств заключается в выражении сложных выражений через ХФ входящих в них множеств. Тождество справедливо, если ХФ левой и правой части уравнения совпадают.

Пример 1. Справедливо ли тождество: (АóВ)∩С = (А∩С) ó (В∩С)?

Слева: χ_АΔВ χ_С = (χ_А + χ_В – 2χ_А · χ_В) χ_С = χ_А χ_С + χ_В χ_С – 2χ_А · χ_В χ_С

Справа: χ_А∩С + χ_В∩С – 2 χ_А∩С χ_В∩С = χ_А χ_С + χ_В χ_С – 2χ_А · χ_В χ_С. Выражения совпадают.

Пример 2: Справедливо ли тождество: (А\В)\С = А\(В\С)?

Слева: χ_А – χ_А χ_B\C = χ_А – χ_А χ_B + χ_А χ_B χ_C

Справа: χ_А\B – χ_А\B χ_C = χ_А – χ_А χ_C – χ_А χ_B + χ_А χ_B χ_C.

Этим вычислением доказано, что операции разности \ неассоциативна.