n-арным или n-местным отношением R между множествами А1, А2,…, Аn называется подмножество декартова произведения:
R Í A1 ‰ A2 ‰ … ‰ An
Если A1 = A2 = … = An=А, то говорят об отношении на множестве А.
При n =1 имеем А1ƒА, т.е. унарное отношение есть просто подмножество R Í A. Другими словами, унарное отношение на множестве А задаёт некоторое подмножество, или отдельные элементы множества А.
В арифметике выделены числа 0 и 1, обладающие особыми свойствами. В теории множеств выделенными элементами являются пустое множество и универсум.
Бинарные (двухместные) отношения удобно изображать на плоскости в декартовой системе координат. На оси Ох изображается множество А, на оси Оу – множество В. Тогда А‰В можно представить в виде прямоугольника. Если множества дискретные, то отношение изобразится некоторым подмножеством множества m‰n точек в прямоугольнике. В непрерывном случае отношение может представляться 2-мерным множеством (областью), линией, отдельными точками и произвольными объединениями этих объектов.
Бинарные отношения (a,b) Í R обозначают также R(a,b), aRb, abR и называют из А в В.
Как и всякое множество, отношения можно задавать: А) перечислением элементов, Б) свойством – характеристическим предикатом, В) порождающей процедурой (алгоритмом) — парадоксы Рассела при этом не возникают, т.к. отношения являются подмножествами хорошо определённого множества – декартова произведения.
В частных случаях отношения можно задавать графически – изображением на плоскости, в виде таблицы и в виде ориентированного графа.
На плоскости R2 отношениями являются =, <, >. = и т.п.: x<y, x=y, x<y, xy=1, …и т.п.
Пусть A={a,b,c}, B={x,y}, R={<a,x>, <a,y>, <b,y>, <c,x>}.
Данное отношение можно задать также следующими способами:
| y | ● | ● | ○ |
| x | ● | ○ | ● |
| a | b | c |

Назовём n-местное отношение R полным, или универсальным, если R= A1 ‰ A2 ‰ … ‰ An.
Назовём отношение R пустым, если R=¯. Эти соответствия называют тривиальными, и они определены для любых множеств.
Если на одном и том же декартовом произведении множеств определены несколько отношений, то к ним можно применять теоретико-множественные операции. При этом пустое и полное отношения играют роль пустого и универсального множества. Следовательно, для произвольных отношений R, R1, R2 на декартовом произведении A1 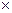 A2
A2 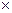 …
… 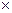 An определены отношения R1ÇR2,R1∩R2, R и т.д. и т.п. Следовательно, на данном декартовом произведении множеств отношения образуют алгебру, которая называется алгеброй отношений.
An определены отношения R1ÇR2,R1∩R2, R и т.д. и т.п. Следовательно, на данном декартовом произведении множеств отношения образуют алгебру, которая называется алгеброй отношений.
 2015-06-24
2015-06-24 680
680








