Совокупность булеана 2Ô и определённых на нём теоретико-множественных операций {Ç, È, \, ó, ¯, …}, называется алгеброй подмножеств.
Подобно тому, как в алгебре действительных чисел некоторое число можно получить (вычислить) разными способами, так и в теории множеств один и тот же результат (множество) может быть получен различными способами. Например, множество–разность можно выразить через пересечение и дополнение:
А\B=AÈB.
Соотношения, связывающие между собой результаты применения различных операций алгебры, называются тождествами алгебры. Основными тождествами алгебры теории множеств являются следующие:
| Идемпотентность | A Ç A = A | A ∩ A = A |
| Коммутативность | A Ç B = B Ç A | A∩B = B ∩ A |
| Ассоциативность | (A Ç B) Ç C = A Ç (B Ç C) | A ∩ (B ∩ C) = (A ∩ B) ∩ C |
| Дистрибутивность | (A Ç B) ∩ C = (A ∩ C) Ç (B ∩ C) | (A∩B) Ç C = (A Ç C) ∩ (B Ç C) |
| Инволютивность | 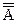 | |
| Свойства дополнения | A ÇĀ | A ∩Ā = ¯ |
| Свойства нуля | А Ç ¯ = A | A ∩ ¯ = ¯ |
| Свойства единицы | A Ç Ô = Ô | A ∩ Ô = A |
| Законы Де Моргана | 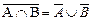 | 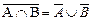 |
| Поглощение | (A ∩ B) Ç А = A | A ∩ (B Ç А) = A |
Данные законы (тождества) алгебры подмножеств не независимы. В аксиоматической теории множеств некоторые из них принимаются за аксиомы, а остальные выводятся из аксиом.
В интуитивном подходе их необходимо доказывать. Проверку этих, а также более сложных тождеств целесообразно проводить с помощью диаграмм Эйлера-Венна, пользуясь сформулированными правилами. Конструктивные же доказательства проводятся с использованием принципа объёмности (аксиома экстенсиональности). Метод состоит в том, что доказываются поочерёдно включения левой части равенства в правую и правой в левую. Называется это методом двух включений. (Докажем, что множества в левой и правой частях равны. Пусть х – любой элемент левой части равенства. Тогда … – поэтому х входит в правую часть. Обратно, пусть х – любой элемент правой части равенства …)
После доказательства тождеств их можно использовать для преобразования произвольных, сколь угодно сложных выражений и приведения их к некоторому стандартному виду. Здесь возникают естественные вопросы: а зачем вообще надо преобразовывать выражения и что такое стандартный вид? Ответим сначала на первый вопрос.
Существует огромное количество практических задач, непосредственно формулируемых на теоретико-множественном языке. В простейших из этих задач необходимо из исходных данных выбрать те, которые удовлетворяют определённым условиям (предикат!), затем отсортировать их по каким-то признакам (снова предикаты). В конечном счёте решение можно записать в виде громоздкого теоретико-множественного выражения. Естественно ожидать, что длинные выражения допускают упрощения, как это происходит в обычной алгебре.
На этом этапе проявляется вторая сложность: неоднозначность полученных выражений. Для разрешения этой проблемы и необходим некоторый «стандартный» вид формул, при приведении к которому можно сравнивать между собой различные теоретико-множественные выражения. Прежде всего следует отметить, что введенных операций слишком много, и это усложняет жизнь. Так, разность, и все остальные бинарные операции можно выразить через пересечение, объединение и дополнение. Формулы, записанные с помощью этих трёх операций, называют формулами в стандартном базисе { Ç, ∩, ¯}.
Алгоритм приведения к стандартному базису можно записать следующим образом:
1. Выразить все операции через стандартные.
2. Используя законы инволютивности ( = A) и де Моргана, добиться того, чтобы дополнения стояли только над обозначениями множеств.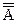
3. Раскрыть скобки и привести к виду «сумма произведений».
4. Из одинаковых слагаемых удалить все, кроме одного; удалить слагаемые, в которых встречается А∩Ā. – Полученное выражение называется формулой в дизъюнктивной нормальной форме (ДНФ).
5. Использовать свойство склеивания (в обратную сторону), чтобы получить одинаковое число «сомножителей» в каждом «слагаемом», например:
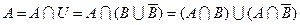
6. Еще раз удалить одинаковые слагаемые, оставив по одному.
7. Полученное выражение называется формулой в совершенной ДНФ (СДНФ).
 2015-06-24
2015-06-24 2376
2376
