2015-06-24
450
1○. Пусть F = < F; +, ‰; 0, 1> – некоторое поле с аддитивной единицей 0 и мультипликативной единицей 1. Элементы поля F: a, b, …Î F называются скалярами.
Пусть V = < V,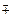 
, 
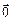> – некоторая коммутативная группа с операцией 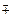. Элементы 
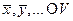называются векторами.
Если существует операция ×: F‰V#V, т.е. функция от двух разносортных переменных с векторными значениями,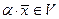 
, удовлетворяющая следующим условиям:
1) 
;
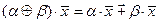2) 
;
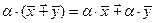3) 
;
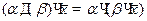4) 
,
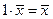то V называется векторным пространством над полем F, а операция × называется умножением на скаляр.
Для векторного пространства справедливы известные теоремы из линейной алгебры.
2○. Нуль-вектор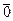 
– единица группы V.
Теорема: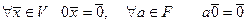 
3○. Линейной комбинацией множества S векторов линейного пространства называется сумма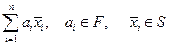 
.
Если из условия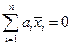 
следует а 1 = а 2 = … = a n =0, то множество 
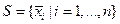называется линейно-независимым. В противном случае, т.е. если существует ненулевой набор a i, зануляющих линейную комбинацию, множество векторов называется линейно-зависимым.
Теорема. Линейно-независимое множество не содержит нуль-вектора.
4○. Базис и размерность.
Линейно-независимое множество векторов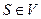 
, такое, что любой элемент V может быть представлен в виде линейной комбинации элементов S, называется базисом пространства V.
Теорема. Каждый элемент векторного пространства имеет единственное представление в данном базисе.
Теорема. Пусть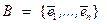 
– базис, а 
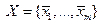– любое линейно-независимое множество. Тогда n ≥ m.
ã Предположим, что m>n. Из того, что В – базис, следует, что любой вектор из Х разлагается по нему, а из того, что F – поле следует, что и базисные векторы разлагаются по n векторам Х. Тогда (n +1)-й вектор Х разлагается по первым n векторам Х, т.е. множество Х – линейно-зависимое. â
Теорема. Пусть В1 и В2 – базисы векторного пространства V. Тогда | В1 | = | В2 |.
Мощность базиса векторного пространства V называется размерностью и обозначается dim(V).
