2015-06-24
1033
Кватернионы вводятся похожим образом – как пары комплексных чисел. Сложение кватернионов покомпонентное, умножение определяется формулой: (a,b)(c,d)=(ac–b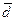 
, ad+b 
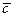). Умножение кватернионов ассоциативно, но не коммутативно. Делителей нуля нет – т.е. по умножению кватернионы образуют группу, а вместе со сложением – тело. Каждый кватернион можно разложить единственным образом по формуле: α = a+bi+cj+dk, где a,b,c,d – действительные числа, i, j, k – мнимые единицы. Умножение кватернионов можно задать таблицей Кэли:
| i | j | k | ||
| i | j | k | ||
| i | i | –1 | k | –j |
| j | j | –k | –1 | i |
| k | k | j | –i | –1 |
— в полной аналогии с векторным произведением векторов в 3-мерном пространстве.
Сопряжение кватерниона – изменение знака у мнимых единиц: α →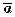 
= a–bi–cj–dk. Норма кватерниона – сумма квадратов компонент (или сумма модулей комплексных чисел, образующих кватернион) – обладает свойствами: 
.
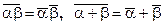Существует изоморфизм между кватернионами и комплексными матрицами 2 на 2 определённого вида. Эти матрицы осуществляют, как говорят, представление кватернионов и называются матрицами Дирака. Соответствие между мнимыми единицами и матрицами Дирака следующее:
Коэффициент при единичной матрице – действительная часть кватерниона.
