Упражнение 25. Простому

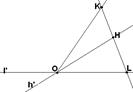
Пусть k, h и l – лучи, выходящие из одной точки О, причём k и h лежат по одну сторону от прямой l¢. Тогда либо k лежит внутри Ð(l,h), а h лежит вне Ð(l,k), либо h лежит внутри Ð(l, k), а k лежит вне Ð(l,h). (Assume kÏÐ(l,h). Prove, that if we chose arbitrary points K and L on k and l correspondingly, segment KL meets line h¢ at some point H. Prove that HÎh and finish the proof)

Def. Многоугольник, имеющий 3, 4,…,n сторон, называется, соответственно, треугольником, четырехугольником, n-угольником. Если

а) все вершины многоугольника различны,

б) ни одна из вершин не лежит на его стороне и

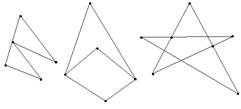
в) никакие две стороны не имеют общих внутренних точек[3], то такой многоугольник называется простым. Примеры многоугольников, не являющихся простыми, приведены на рисунках.

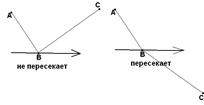Пусть у нас имеется простой многоугольник и его пересекает луч или прямая. Подсчитаем число пересечений прямой (луча) с многоугольником по следующему правилу: за одно пересечение будем считать либо

a) пересечение с отрезком, служащим стороной многоугольника, либо

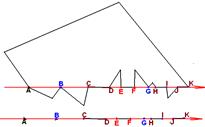
b) 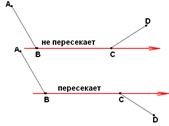прохождение через вершину В, если при этом стороны ВА и ВС, исходящие из этой вершины окажутся по разные стороны луча, либо

c) прохождение по стороне ВС многоугольника (т.е., через две его соседние вершины), при условии, что две соседних с ней стороны (т.е., точки: предшествующая В и следующая за С) находятся по разные стороны от луча.

Будем временно считать углом любую пару лучей, исходящих из одной точки, даже в случае, когда они образуют прямую линию (развёрнутый угол). В этом случае, под внутренностью угла будем понимать произвольно выбранную полуплоскость (одну из двух, на которые делит плоскость такой угол).

Упражнение 26*.

Все точки плоскости, не принадлежащие простому многоугольнику Т, делятся им на два класса: на те, все лучи, исходящие из которых пересекают Т чётное число раз и те, все лучи, исходящие из которых пересекают Т нечётное число раз. То есть, если например, какой-то луч, выходящий из некоей точки О пересекает Т чётное число раз, то и любой другой луч выходящий из Т также пересечёт Т чётное число раз.

(two rays, h and k make angle (h,k). Let’s take away all points where either of rays intersects polygon T, including those sides of T which lie on either ray crossing through the T. Now T disintegrated into pieces. Prove that number of these pieces is always even)

Def. Точки, лучи из которых пересекают данный простой многоугольник нечётное число раз, назовём его внутренними точками, остальные точки (исключая точки самого многоугольника), назовём его внешними точками.

Пусть из точки О выходит луч h, который k раз пересекает стороны многоугольника Т, l раз пересекает его в его вершинах, р раз проходит через его вершины, не пересекая Т, m раз проходит через его стороны, пересекая Т и q раз проходит через его стороны, не пересекая Т. Тогда число пересечений лучом многоугольника равно k+l+m, на луче лежат 2(m+q) концов сторон многоугольника, l+p его вершин и k точек пересечения со сторонами в их внутренних точках. Всего, считая вместе с О, k+l+p+2(m+q)+1 точек, расположенных в определенном порядке. Перенумеруем их, начиная от О в соответствии с упражнением 8. Перенумеруем и пересечения с Т. Если i-ое пересечение представляет собой отрезок – сторону FG многоугольника, а предыдущей общей точкой луча и многоугольника была Е, а последующей – Н, то отрезки ЕF и GH не содержат ни одной точки многоугольника. То же самое было бы если бы пересечение стороны или вершины многоугольника проходило в одной точке. Все точки, лежащие на отрезках луча, не имеющих с многоугольником ни одной общей точки, одновременно находятся все внутри многоугольника либо все вне него. Более того, поскольку речь идёт о пересечении многоугольника, то отрезки луча, не имеющие общих точек с многоугольником, непосредственно предшествующие пересечению и непосредственно следующие за ним чередуются: либо первый состоит из внутренних точек, а второй из внешних, либо наоборот.