Упражнение 60

Все прямые углы конгруэнтны между собой.

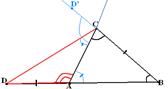Def. Угол, больший своего смежного (и, следовательно, больший прямого угла), называется тупым. Угол, меньший своего смежного (и, следовательно, меньший прямого угла), называется острым. Принадлежащие треугольнику АВС углы АВС, ВСА и САВ называются углами этого треугольника, углы, смежные к этим углам, называются внешними углами треугольника.

Упражнение 61*. (Теорема о внешнем угле)

Внешний угол треугольника больше каждого из двух не смежных с ним углов. Как это часто бывает в геометрии, здесь вновь оказываются полезными дополнительные построения. Отложите на стороне 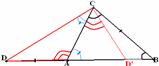AD ÐСАD (смежного углу САВ) отрезок АDºСВ. Докажите, что не может быть ни ÐСАDºÐАСВ, ни ÐСАD<ÐАСВ. (the second follows from the first once it is proved – look on the picture at the left and apply it to ACD¢. For the second inequality address to the angle, vertical to ÐСАD)