2015-06-24
422
Дифференциальные уравнения
Определение 1. Обыкновенным дифференциальным уравнением n –ого порядка называется соотношение вида: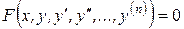 
(1),
где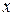 
– независимая переменная; 
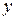– искомая функция переменной;
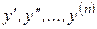– производные искомой функции; 
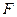– известная функция своих аргументов.
Считается, что производная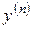 
на самом деле входит в выражение (1), а величины 
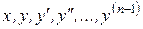могут и не входить в него.
Определение 2. Порядком дифференциального уравнения, n, называется наивысший порядок производной, входящей в это уравнение.
Пример.
1) 
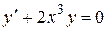– уравнение первого порядка;
2) 
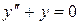– уравнение второго порядка;
3) 
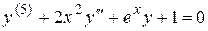– уравнение пятого порядка.
Определение 3. Всякая функция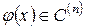 
, которая, будучи подставленная вместо y в выражение (1), обращает это выражение в тождество, называется решением дифференциального уравнения (1).
Если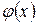 
– решение, то по определению
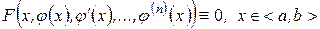(2)
Пример.
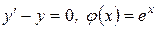– решение, так как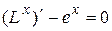 
У рассматриваемого уравнения есть еще такое решение: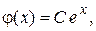 
где С – произвольная постоянная.
Это значит, что это уравнение имеет бесчисленное множество решений, зависящих от одного параметра (С).
|
|
|
Можно показать, что уравнение n –ого порядка имеет семейство решений, зависящих от произвольных независимых друг от друга постоянных.
