2015-06-24
501
Практические задания
1. Найти область определения функции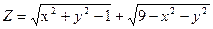 
.
; 
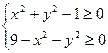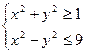
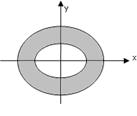
Областью определения функции является кольцо, включая границы окружности.
2. Вычислить предел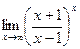 
.
Второй замечательный предел
, 
.
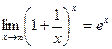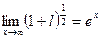
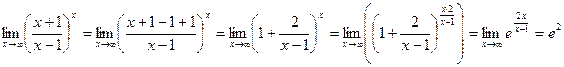
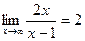3. Найти дифференциал второго порядка от функции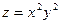 
.
, 
, 
,
, 
,
.
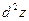
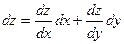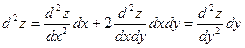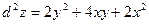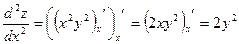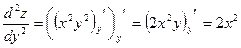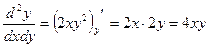4. Вычислить производную функции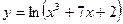 
.
.
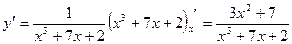5. Найти производную от неявной функции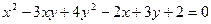 
.
, 
,
,
.
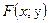
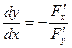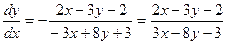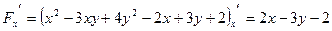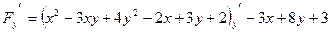6. Найти экстремумы функции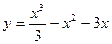 
и построить схематический график.
; 
,
; 
, 
.
,
,
,
; 
, 
, 
.
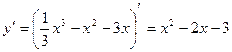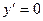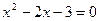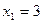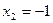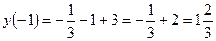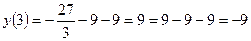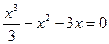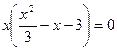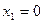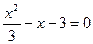
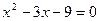
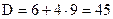
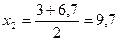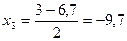7. Найти интервалы выпуклости, вогнутости и точки перегиба графика функции: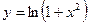 
.
; 
;
;
;
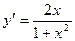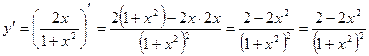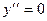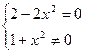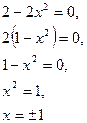
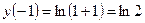- точка перегиба
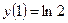- точка перегиба
8. Найти и исследовать точки разрыва функции: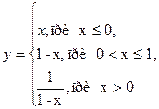 
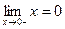, в точке 
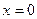скачок.
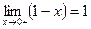, в точке 
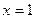- разрыв.
|
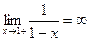
9. Найти неопределённый интеграл: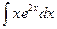 
.
Найдем неопределенный интеграл методом интегрирования по частям. Используя формулу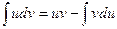 
.
.
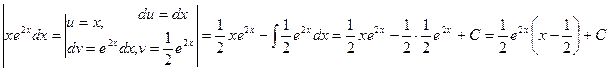10. Вычислить определённый интеграл: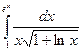 
.
Вычислим определенный интеграл методом подстановки.
,
,
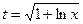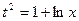
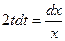если 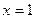, то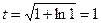 
если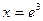 
, то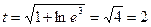 
.
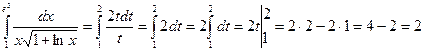11. Вычислить площадь плоской области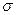 
, ограниченной линиями 
, 
, 
.
|
|
|
, ,
, 
, 
.
, , 
, 
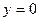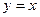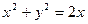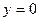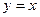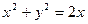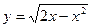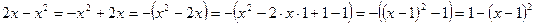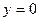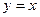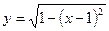
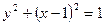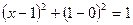
Окружность (1;0) с радиусом R=1.
,
,
.
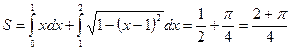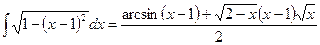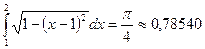12. Исследовать на сходимость числовой ряд: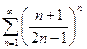 
.
Радикальный признак Коши.
, 
.
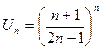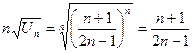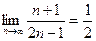- ряд сходится.
13. Найти область сходимости степенного ряда: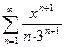 
.
,
,
, 
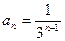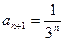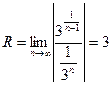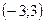
Пусть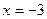 
, получим ряд 
.
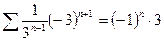Исследуем ряд по признаку Лейбница, т.к. он знакочередующийся.
а) по первому признаку Лейбница каждый последующий член ряда по абсолютной величине должен быть меньше предыдущего, т.е. в нашем случае условие не выполняется, так как 3=3=3
б) По второму признаку Лейбница предел ряда должен стремиться к нулю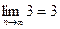 
второе условие выполняется. Ряд расходится, значит 
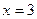- точка расходимости.
При 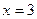получим ряд
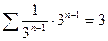- числовой знакоположительный ряд. Исследуем его сходимость при помощи интегрального признака сходимости коши.
Рассмотрим несобственный интеграл:
несобственный интеграл расходится и следовательно расходится и исследуемый ряд.
Значит 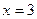- точка расходимости.
Степенной ряд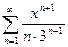 
, сходится, при 
.
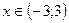14. Найти частное решение дифференциального уравнения: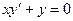 
при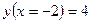 
.
,
,
: 
.
, 
,
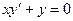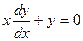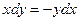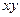
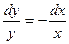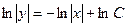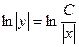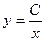- семейство гипербол.
; 
,
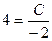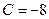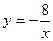- частное решение исходного уравнения.
15. Найти длину астроиды: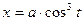 
, 
.
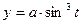Кривая симметрична относительно обеих осе, следовательно, вычислим длину её четвёртой части, расположенной в I квадрате:
,
,
,
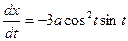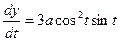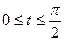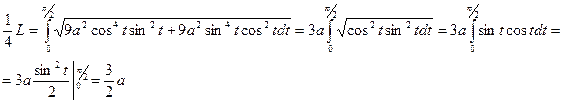
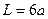- длина астроиды
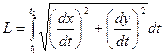- длина дуги кривой, если кривая задана параметрическим уравнением.
