Количество теплоты, отдающееся с нагретой поверхности, зависит от условий конвективного теплообмена. Для расчета количества теплоты используются критериальные уравнения, полученные на основе рассмотрения подобных явлений.
В общем виде критериальное уравнение теплоотдачи конвекцией может быть представлено в следующей форме:
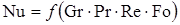 , (1.15)
, (1.15)
где 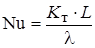 – критерий Нуссельта; (1.16)
– критерий Нуссельта; (1.16)
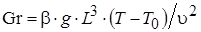 – критерий Грасгофа; (1.17)
– критерий Грасгофа; (1.17)
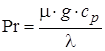 – критерий Прандтля; (1.18)
– критерий Прандтля; (1.18)
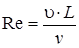 – критерий Рейнольдса; (1.19)
– критерий Рейнольдса; (1.19)
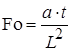 – критерий Фурье; (1.20)
– критерий Фурье; (1.20)
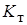 – коэффициент теплоотдачи конвекцией, Вт/(м2?К);
– коэффициент теплоотдачи конвекцией, Вт/(м2?К); 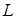 – характерный геометрический размер тела (диаметр цилиндра, шара, высота вертикальной поверхности и т.п.), м;
– характерный геометрический размер тела (диаметр цилиндра, шара, высота вертикальной поверхности и т.п.), м; 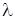 – коэффициент теплопроводности, Вт/(м?К);
– коэффициент теплопроводности, Вт/(м?К); 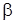 – коэффициент объемного расширения, К-1;
– коэффициент объемного расширения, К-1; 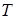 – температура поверхности, °С;
– температура поверхности, °С; 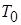 – температура окружающей среды, °С;
– температура окружающей среды, °С; 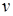 – коэффициент кинематической вязкости жидкости или газа, м2/с;
– коэффициент кинематической вязкости жидкости или газа, м2/с; 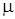 – коэффициент динамической вязкости жидкости или газа, Н?с/м2;
– коэффициент динамической вязкости жидкости или газа, Н?с/м2; 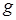 – ускорение силы тяжести, м/с2;
– ускорение силы тяжести, м/с2; 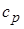 – удельная теплоемкость жидкости или газа при постоянном давлении, Дж/(кг?К);
– удельная теплоемкость жидкости или газа при постоянном давлении, Дж/(кг?К); 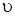 – скорость, м/с;
– скорость, м/с; 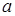 – коэффициент температуропроводности, м2/с;
– коэффициент температуропроводности, м2/с; 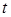 – время, с.
– время, с.
|
|
|
Приведем некоторые критериальные уравнения для различных условий теплопередачи конвекцией с поверхности частей электрических аппаратов.
1. Свободная конвекция в неограниченном пространстве [1]:
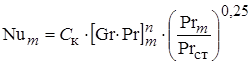 . (1.21)
. (1.21)
Индексы “ 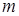 ” и “
” и “  ” означают, что при вычислении критериев подобия физические параметры необходимо брать при температуре
” означают, что при вычислении критериев подобия физические параметры необходимо брать при температуре 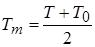 и температуре стенки
и температуре стенки 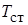 соответственно.
соответственно.
Величины 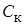 и
и 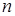 определяются по табл. 1.2 [1].
определяются по табл. 1.2 [1].
Таблица 1.2. Коэффициенты 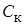 и
и 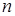
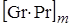 | 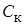 | 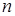 |
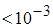 | 0,5 | |
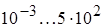 | 1,18 | 0,125 |
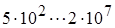 | 0,54 | 0,25 |
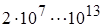 | 0,135 | 0,33 |
Примечание: При использовании формулы (1.21) для горизонтальных плит полученный коэффициент теплоотдачи необходимо увеличить на 30% для верхней плоскости плиты и уменьшить на 30% для нижней плоскости.
Рассмотрим пример расчета теплоотдачи свободной конвекцией в неограниченное пространство.
Пример. Определить коэффициент теплоотдачи конвекцией с боковой наружной поверхности цилиндрической катушки индуктивности высотой 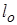 =200 мм, расположенной вертикально в спокойном воздухе, температура которого
=200 мм, расположенной вертикально в спокойном воздухе, температура которого 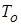 =35 °С. Катушка достаточно удалена от других аппаратов. В результате протекания по ней тока температура ее поверхности составила
=35 °С. Катушка достаточно удалена от других аппаратов. В результате протекания по ней тока температура ее поверхности составила 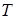 =105 °С.
=105 °С.
Решение. Для свободной конвекции можно воспользоваться формулой (1.21) для определения коэффициента теплоотдачи, так как для воздуха 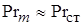 , то формула примет следующий вид:
, то формула примет следующий вид:
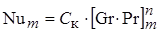 .
.
Для определения коэффициентов 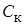 и
и 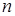 вычислим произведение
вычислим произведение 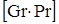 при
при 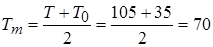 °С.
°С.
Значения физических параметров воздуха при температуре 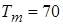 °С (см. табл. П.9):
°С (см. табл. П.9):
|
|
|
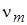 =20,02?10-6м2/с;
=20,02?10-6м2/с;
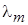 =2,96?10-2 Вт/(м?К);
=2,96?10-2 Вт/(м?К);
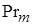 =0,694;
=0,694;
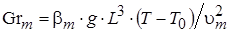 ; (1.22)
; (1.22)
для воздуха 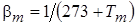 =1/(273+70)=1/347?К-1;
=1/(273+70)=1/347?К-1;
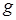 =9,81 м/с.
=9,81 м/с.
В качестве определяющего размера примем высоту катушки 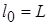 =0,2м.
=0,2м.
Тогда, используя выражение (1.22), получим:
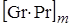 =9,81?0,23?(105-35)?0,694/[347? (20,02?10-6)2]=2,74?107.
=9,81?0,23?(105-35)?0,694/[347? (20,02?10-6)2]=2,74?107.
Из табл. 1.2 определяем 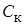 =0,135;
=0,135; 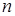 =1/3.
=1/3.
Тогда 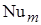 =0,135?(2,74?107)1/3=40,7, откуда из формулы (1.21):
=0,135?(2,74?107)1/3=40,7, откуда из формулы (1.21):
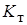 =40,7?2,96?10-2/0,2=6,02 Вт/(м2?К).
=40,7?2,96?10-2/0,2=6,02 Вт/(м2?К).
2. При расчете теплоотдачи конвекцией в ограниченном пространстве (стесненной конвекцией) [1] полагают, что теплоотдача происходит практически теплопроводностью через среду, имеющую эквивалентный коэффициент теплопроводности 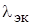 , определяемый из соотношения:
, определяемый из соотношения:
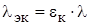 , (1.23)
, (1.23)
где 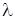 – действительный коэффициент теплопроводности, определяемый по среднеарифметической температуре стенок
– действительный коэффициент теплопроводности, определяемый по среднеарифметической температуре стенок 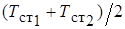 , Вт/(м?К);
, Вт/(м?К); 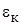 – коэффициент конвекции, определяемый из критериальных уравнений (табл. 1.3).
– коэффициент конвекции, определяемый из критериальных уравнений (табл. 1.3).
Таблица 1.3. Коэффициент конвекции
| № п/п | 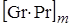 | Критериальное уравнение | Номер уравнения |
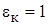 1.24 1.24 | |||
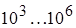 | 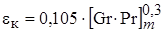 | 1.25 | |
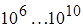 | 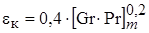 | 1.26 |
В критерий Грасгофа входит разность температур между стенками.
Тепловой поток конвективного теплообмена 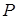 , Вт, в ограниченном пространстве определяется по формуле:
, Вт, в ограниченном пространстве определяется по формуле:
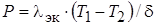 , (1.27)
, (1.27)
где 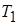 и
и 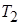 – температуры поверхностей, принимающих участие в теплообмене, °С;
– температуры поверхностей, принимающих участие в теплообмене, °С; 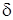 – характерный линейный размер (расстояние между поверхностями), м.
– характерный линейный размер (расстояние между поверхностями), м.
Далее приведен пример теплового расчета для случая стесненной конвекции.
Пример. Определить эквивалентный коэффициент теплопроводности и плотность теплового потока между двумя вертикальными плоскими стенками, находящимися на расстоянии 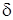 =10 мм друг от друга, если известно, что температуры стенок соответственно
=10 мм друг от друга, если известно, что температуры стенок соответственно 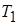 =150 °С,
=150 °С, 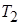 =35 °С, а между стенками находится спокойный воздух.
=35 °С, а между стенками находится спокойный воздух.
Решение. Для условной стесненной конвекции воспользуемся уравнением (1.23), в котором определяющая температура равна:
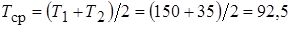 °С.
°С.
При этой температуре определяем из табл. П.9 параметры воздуха:
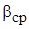 =1/366 К-1;
=1/366 К-1; 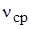 =22,4?10-6м2/с;
=22,4?10-6м2/с; 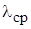 =3,15?10-2 Вт/(м?К);
=3,15?10-2 Вт/(м?К); 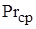 =0,69.
=0,69.
Тогда, используя формулу (1.22), получим
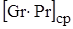 =(1/366)?9,81?115?0,69?(10-2)3/(22,4?10-6)2=4239.
=(1/366)?9,81?115?0,69?(10-2)3/(22,4?10-6)2=4239.
В этом случае справедливо критериальное уравнение (1.25) из табл. 1.3:
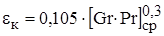 =0,105?42390,3 =1,29.
=0,105?42390,3 =1,29.
Эквивалентный коэффициент теплопроводности
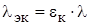 =1,29?3,15?10-2=4,06?10-2Вт/(м?К).
=1,29?3,15?10-2=4,06?10-2Вт/(м?К).
Из закона теплопроводности Фурье (1.27) определим плотность теплового потока:
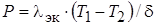 =4,06?10-2?(150-35)/10-2=467 Вт/м2.
=4,06?10-2?(150-35)/10-2=467 Вт/м2.
3. Критериальные уравнения вынужденной конвекции при движении жидкости или газа вдоль плоской стенки [2]:
а) для 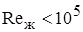 (ламинарный режим):
(ламинарный режим):
- при обтекании жидкостью
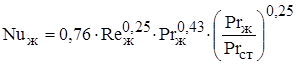 ; (1.28)
; (1.28)
- при обтекании газом (воздухом)
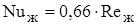 ; (1.29)
; (1.29)
б) для 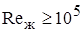 (турбулентный режим)
(турбулентный режим)
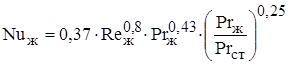 , (1.30)
, (1.30)
где 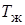 – температура в начале стенки по отношению к набегающему потоку, °С;
– температура в начале стенки по отношению к набегающему потоку, °С; 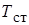 – средняя температура поверхности стенки, °С;
– средняя температура поверхности стенки, °С;
За определяющий размер принимают длину стенки по направлению движения потока.
4. Теплоотдача вынужденной конвекцией при протекании жидкости или газа в гладких трубах:
а) для 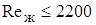 (ламинарный режим)
(ламинарный режим)
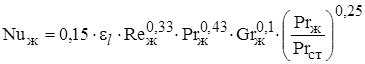 , (1.31)
, (1.31)
где 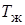 и
и 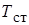 – соответственно средние значения температур жидкости или газа и поверхности трубы, °С,
– соответственно средние значения температур жидкости или газа и поверхности трубы, °С,
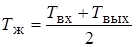 , (1.32)
, (1.32)
где 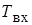 и
и 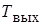 – соответствующие температуры жидкости или газа на входе трубы и на ее выходе, °С.
– соответствующие температуры жидкости или газа на входе трубы и на ее выходе, °С.
За определяющий размер принимается внутренний диаметр трубы.
Коэффициент 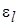 определяется из табл. 1.4, в которой
определяется из табл. 1.4, в которой 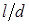 – отношение длины трубы к ее внутреннему диаметру.
– отношение длины трубы к ее внутреннему диаметру.
Таблица 1.4. Коэффициент 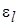
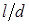 | |||||||||
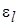 | 1,90 | 1,70 | 1,44 | 1,28 | 1,18 | 1,13 | 1,05 | 1,02 | 1,00 |
б) для 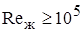 (турбулентный режим)
(турбулентный режим)
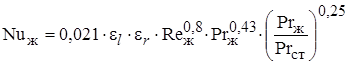 , (1.33)
, (1.33)
где 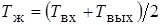 , – температура стенки трубы, °С.
, – температура стенки трубы, °С.
Коэффициент 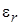 , учитывающий влияние закругления трубы, выпол-ненной в виде змеевика, определяют по формуле
, учитывающий влияние закругления трубы, выпол-ненной в виде змеевика, определяют по формуле
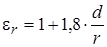 , (1.34)
, (1.34)
где 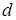 – внутренний диаметр трубы, м;
– внутренний диаметр трубы, м; 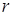 – радиус закругленной трубы, м.
– радиус закругленной трубы, м.
Значения 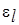 определяют из табл. 1.5.
определяют из табл. 1.5.
Таблица 1.5. Коэффициент 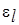
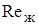 | Значение 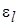 при отношении при отношении 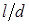 | ||||||||
| 104 | 1,65 | 1,50 | 1,34 | 1,23 | 1,17 | 1,13 | 1,07 | 1,03 | 1,0 |
| 2?104 | 1,51 | 1,40 | 1.27 | 1,18 | 1,13 | 1,10 | 1,05 | 1,02 | 1,0 |
| 5?104 | 1,34 | 1,27 | 1,18 | 1,13 | 1,10 | 1,08 | 1,04 | 1,02 | 1,0 |
| 105 | 1,28 | 1,22 | 1,15 | 1,10 | 1,08 | 1,06 | 1,03 | 1,02 | 1,0 |
| 106 | 1,14 | 1,11 | 1,08 | 1,05 | 1,04 | 1,03 | 1,02 | 1,01 | 1,0 |
Рассмотрим расчет теплоотдачи вынужденной конвекцией на следующем примере.
|
|
|
Пример. Определить допустимую силу тока и необходимый расход воды для медной круглой шины длиной 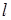 =5 м, если известно, что внутренний диаметр шины
=5 м, если известно, что внутренний диаметр шины 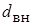 =45 мм, наружной
=45 мм, наружной 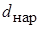 =50 мм, температура воды на входе
=50 мм, температура воды на входе 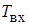 =25 °С, а допустимая температура воды на выходе
=25 °С, а допустимая температура воды на выходе 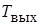 =55 °С. Температура внутренней стенки шины не должна превышать
=55 °С. Температура внутренней стенки шины не должна превышать 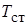 =90 °С.
=90 °С.
Решение. Средняя температура воды
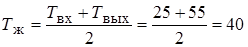 °С.
°С.
Энергия, уносимая водой в единицу времени,
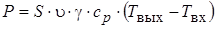 ,
,
где 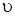 – скорость движения воды в трубе, м/с;
– скорость движения воды в трубе, м/с; 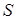 – площадь поперечного сечения трубы, м2;
– площадь поперечного сечения трубы, м2; 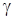 – удельный вес воды, кг/м3.
– удельный вес воды, кг/м3.
Для определения характера течения воды необходимо знать величину критерия Рейнольдса. Определим скорость движения воды из полученного выше выражения:
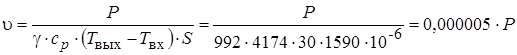 ,
,
где 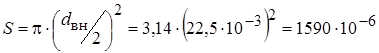 м2;
м2; 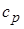 =4174 Дж/(кг?К);
=4174 Дж/(кг?К); 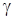 =992 кг/м3.
=992 кг/м3.
Тогда критерий Рейнольдса
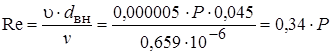 ,
,
где коэффициент кинематической вязкости жидкости 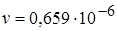 м2/с.
м2/с.
Так как 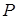 неизвестна, то определяем характер режима течения воды методом подбора. Допустим, что режим течения ламинарный. В этом случае режим описывается критериальным уравнением (1.31):
неизвестна, то определяем характер режима течения воды методом подбора. Допустим, что режим течения ламинарный. В этом случае режим описывается критериальным уравнением (1.31):
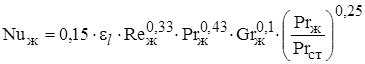 ,
,
где 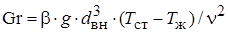 =[3,87?10-4?9,81?(45?10-3)3?50]/(0,659?10-6)2= =39831?103;
=[3,87?10-4?9,81?(45?10-3)3?50]/(0,659?10-6)2= =39831?103; 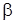 – коэффициент объемного расширения, равный 3,87?10-4 К-1.
– коэффициент объемного расширения, равный 3,87?10-4 К-1.
Тогда
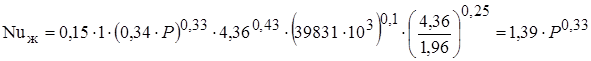 ,
,
так как для прямой трубы 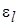 =1 при
=1 при 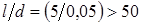 (табл. 1.4).
(табл. 1.4).
Энергия, отдаваемая трубой воде и уносимая ею в единицу времени:
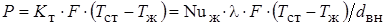 ,
,
где 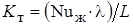 – коэффициент теплообмена;
– коэффициент теплообмена; 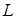 – определяющий размер, выбирается равным внутреннему диаметру трубы
– определяющий размер, выбирается равным внутреннему диаметру трубы 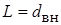 ;
; 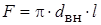 – площадь внутренней поверхности трубы, м2;
– площадь внутренней поверхности трубы, м2; 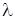 – коэффициент теплопроводности воды при
– коэффициент теплопроводности воды при 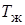 =40 °С, Вт/(м?К).
=40 °С, Вт/(м?К).
Тогда
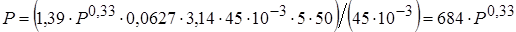 ,
,
откуда 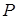 =565,7 Вт.
=565,7 Вт.
Проверим величину критерия Рейнольдса:
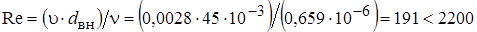 ,
,
где 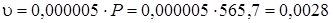 м/с.
м/с.
Значит, режим течения воды ламинарный.
Определяем расход воды:
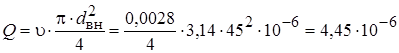 м3/с.
м3/с.
 2015-06-24
2015-06-24 17772
17772
